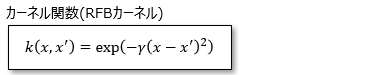カーネル法(カーネル関数)とは　pythonでの回帰分析

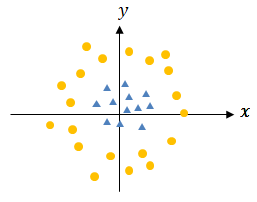
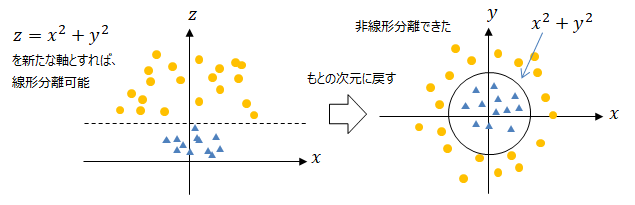
カーネル法とは、非線形分離(回帰)問題を解く手法の一つで、データを高次元空間に写像することで線形分離(回帰)した後、元の低次元空間に戻すことで非線形分離(回帰)を行います。高次元空間への写像を行い線形分離を行う場合、内積(共分散)の計算が必要になり膨大な計算量になるのですが、カーネル関数を用いることで膨大な計算を行うことなく非線形分離できるのが特徴です。これをカーネルトリックともいいます。

線形分離のイメージについて説明します。例えば以下の様なデータは、このままでは線形分類できません。

これを以下の様にZ軸(=x²+y²)という新たなパラメータで表すと線形分離可能となり、その状態で線形分離した後、再びもとの低次元空間に戻すことで非線形分離が可能となります。なおこの考えを利用して分類を行う方法にサポートベクターマシンがあります。

＜カーネル関数の種類＞
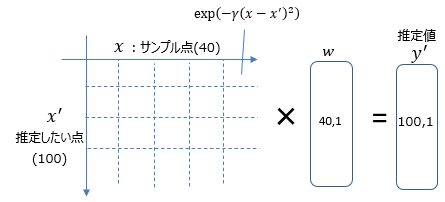
カーネル関数には線形カーネルや多項カーネル、ガウスカーネル、RBF(Radial Basis Function)カーネルなどがあります。RBFカーネルは以下のとおり。

■カーネル法を用いた回帰の手順

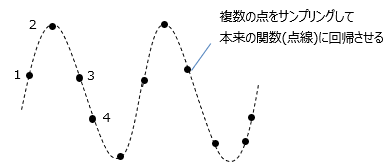
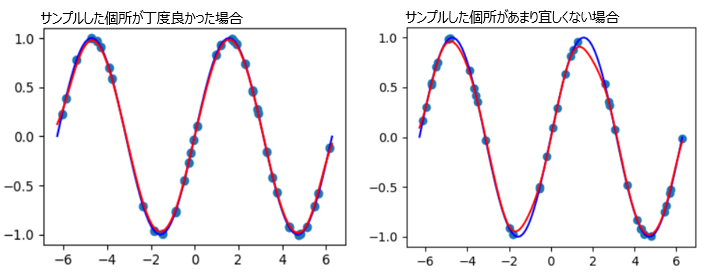
具体例として、サンプルした点からsin波に回帰させる方法を説明します。

＜step①＞
データを(今回は)40点サンプルします。各点に便宜的に番号を振ります。

＜step②＞
各サンプル点xと他の全てのサンプル点x'に対する、カーネル関数の値をそれぞれ求め、その結果を以下行列の様に並べます。これはカーネル行列あるいはグラム行列といい、共分散行列になっておりサンプル点の相関関係を表しています。(サンプル点の値が近い程、出力も近い値になる)

＜step③＞
カーネル行列を使用して以下式に基づいて回帰関数のパラメータwを求めます。

＜step④＞
パラメータwをもとに回帰を行います。各推定したい点x'と全てのサンプル点xに対するカーネル関数の値をそれぞれ求め、それにwをかけたものの和が、推定したい点x'のyの値になります。

■カーネル法を用いた回帰の実装例 (python)

実施した環境とライブラリは以下のとおり。

　・python ver：3.9
　・必要なライブラリ：numpy, matplotlib, itertools　インストール方法

import numpy as np
from matplotlib import pyplot as plt
from itertools import product

def kernel(x, xd):     # カーネル関数
    K = np.zeros([len(x), len(xd)])
    for i, j in product(range(len(x)), range(len(xd))):
        K[i][j] = np.exp(-theta * (x[i]-xd[j])**2)
    return K

N = 40    # サンプル数
lamda  = 0.1
theta   = 1
X_smpl = np.random.uniform(-2*3.14, 2*3.14, N)        # サンプルX値
Y_smpl = np.sin(X_smpl)        # サンプルY値
X_est   = np.linspace(-2*3.14, 2*3.14, 100)    # 推定したいX値

K     = kernel(X_smpl, X_smpl)            # カーネル関数値算出
W    = np.dot(np.linalg.inv(K + lamda * np.eye(N)),Y_smpl)    # パラメータ計算
Y_est = np.dot(kernel(X_est, X_smpl),W)    # 推定値

plt.scatter(X_smpl, Y_smpl)
plt.plot(X_est, np.sin(X_est), c='blue')
plt.plot(X_est, Y_est, c="red")
plt.show()

＜プログラム実行結果＞
結果は以下のとおり。青点がサンプル点、赤線が推定値、青線が本来の線です(赤線と重なって見づらいですが)。サンプルした個所によって推定結果にばらつきが出ますが、おおむね適切に推定できている事が分かります。

サブチャンネルあります。⇒ 何かのお役に立てればと

カーネル法(カーネル関数)とは pythonでの回帰分析

■カーネル法とは

■カーネル法を用いた回帰の手順

■カーネル法を用いた回帰の実装例 (python)

カーネル法(カーネル関数)とは　pythonでの回帰分析