|
前提知識
・二項分布
・背理法
■仮説検定とは
仮説検定とは、仮説の妥当性を統計的推論から検証する手法の一つです。
例えば、コイントスをした際に「オモテ」と「ウラ」の出る確率は半々になると考えますが、仮に10回とも「オモテ」が出た場合、
そのコインにイカサマが施されているかどうかを検証します。
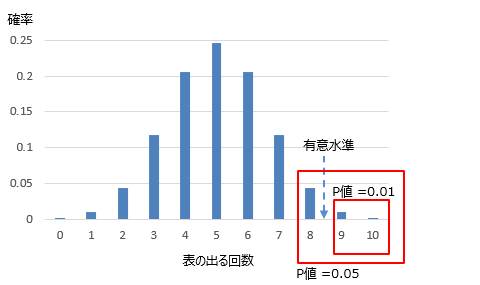
「オモテ」と「ウラ」の出る確率が半々の場合、10回試行した時のそれぞれの出る確率分布は、二項分布を用いると以下となります。

ここで10回とも「オモテ」が出る確率は0.1%と極めて低い確率になっており、もし本当に10回「オモテ」が出たならば、
それはコインのイカサマを疑う方が蓋然性が高いと考えます。(ただし100%イカサマであるとは限りません)
<コインがイカサマだと判断するラインはどこにあるのか>
コインが10回とも「オモテ」の場合はイカサマを疑うのが自然ですが、では10回中9回あるいは8回「オモテ」がでた場合、それはイカサマと考えて良いのでしょうか。
仮説検定では検定対象事象の累積確率(これをp値という)が慣習として0.05(5%)以下であれば、それはイカサマと判断して良いと考えます。
ただし今回の場合「オモテ」が10回出るのと同様に「ウラ」が10回出るのも考えにくいことから、「オモテ」と「ウラ」のp値の合算値0.05を有意水準とします(これを両側検定という)。
つまり「オモテ」側の有意水準は0.025とします。
以上より、
8回の時のP値=0.05
9回の時のP値=0.01
となり、8回までは「オモテ」が出ても有意差があると言えない(イカサマと判断できない)となります。
■仮説検定の正しい手順
上記は仮説検定の考え方ですが、少し形式的にはなりますが仮説検定の正しい手順があります。
<① 帰無仮説を設定する>
帰無仮説とは、無に帰したい(否定したい)仮説のことです。今10回連続で「オモテ」が出たのを目の当たりにしたあなたは「コインはイカサマに違いない」と思います。
従って否定したい仮説(帰無仮説)は「コインがイカサマでない」ということになります。
帰無仮説:コインがイカサマでない
対立仮説:コインがイカサマである
仮説検定は、帰無仮説の「コインがイカサマではない」ことを否定することによって、対立仮説である「コインがイカサマである」という事を証明するという、回りくどいやり方をします。
これは背理法という証明方法で、ある事象が「正しいことを証明する場合」は、それが正しいという材料を全て持ってこなければ証明できませんが、
「正しくない事を証明する場合」は、否定材料を一つ持ってくれば証明できるという利点を持っています。
また帰無仮説を「コインがイカサマである」としたい人もいるかと思いますが。仮説検定では「データに有意がある」という事を証明する場合が多く、
変な言い方ですが「コインがイカサマではないことを否定したく」、帰無仮説は「コインがイカサマではない」とします。
<② 事象の確率分布を求める>
上記図1の様に、コインの表が出る回数の確率分布を求めます。
<③ 検定対象のp値を求める>
今回は、10回連続で出た場合を検定対象としますので、p値は0.001とします。
<④ 検定対象のp値と有意水準を比較する>
以下の関係となります。
有意水準 > p値 ⇒ 有意差があるとし、帰無仮説は棄却する
有意水準 < p値 ⇒ 有意差があるとはいえず、帰無仮説は棄却できない
今回、有意水準0.025 > p値 0.001のため、帰無仮説は棄却され有意差がある、つまり「コインはイカサマ」と考えるのが妥当であると判断します。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|

