データを正しく読む

データやグラフを正しく読むためのコツの様なものを紹介します。これから出てくる例やグラフは簡素化した上で説明してます。

＜具体例①　特性の遅れを知る＞
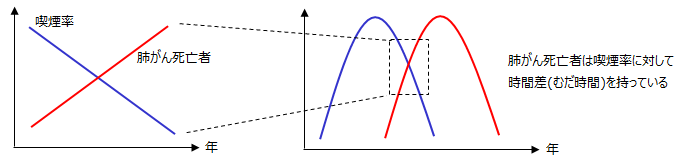
たばこの喫煙率と肺がんで亡くなる人の関係を示したグラフです。左のグラフを見ると、喫煙率が下がるに従い死亡者数が増加している様に見えますが、実はグラフをもっと長いスパンで見ると右グラフの様になります。死亡者は喫煙率に対して時間差(むだ時間)を持っており、ちょうど特性の向きが反対となっている所を拾ったデータが左のグラフとなります。全体の特性を鑑みた結果、喫煙者が増えるに従い肺がん死亡者数は増えるとみるのが正しいです。

＜具体例②　必ずしも外挿部分は線形ではない＞
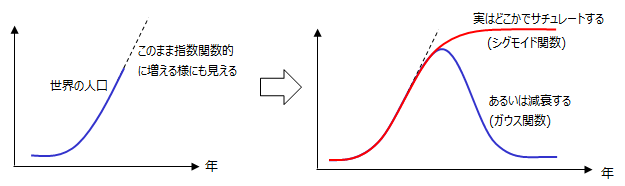
次のグラフは世界の人口を表したグラフです。左のグラフを見ると、このまま指数関数的に人口が増加するようにも見えますが、最近の研究ではどこかでサチュレート(飽和)することが解っております (シグモイド関数)。また人口の事例以外を例にとった場合、減衰する可能性も十分あり得ます(ガウス関数)。人間はグラフの外側を直線で外挿してしまう傾向があるので注意が必要です。

＜具体例③　相関関係と因果関係は異なる＞
世界の人口と自動車台数を表したグラフです。人口が増えるに従い自動車台数も増えているので、両者には相関関係があると言えます。しかし先に自動車をたくさん生産したとしても人口が増えるわけではないので、人口が多い理由(結果)は自動車が多いから(原因)ではない、つまり因果関係は無いと言えます。 (ただし自動車が多い理由は人口が多いからという事は成り立つので因果関係はあります)。

＜具体例④　パレートの法則＞
パレートの法則とはイタリア経済学者ヴィルフレド・パレートによって発見された法則で、全体の数値の大部分(8割)は、全体を構成する一部の要素(2割)の数値によって構成されているという法則で、80:20の法則ともいわれています。パレートの法則の具体例は以下。

　・商品の売り上げの8割は、全顧客の2割で生み出されている。
　・プログラム処理時間の8割は、コード全体の2割の部分が占めている。

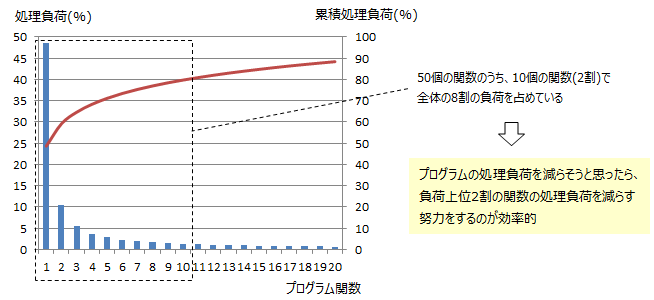
私が実際に経験した事例ですが、マイコンにプログラムを実装しようとした際に、プログラムの処理負荷が高く処理抜けが発生してしまい、負荷を軽く(シュリンク)する必要が出てきました。その際に各関数の処理負荷を分析した際に以下の様(イメージ図です)になっており、パレートの法則に近い状態になっている事が解りました。そこで、負荷の8割を占める2割の関数に注力したので、費用対効果の観点で効率よくシュリンクできました。

ここで重要なのは、注力すべき対象をどこまで広げるかという根拠を一つの考え方をもって示せることです。何も考え無しに、TOP10だけやるとか、半分のTOP25までやると決めるより良いのだと思います。

＜具体例⑤　初歩的なこと＞
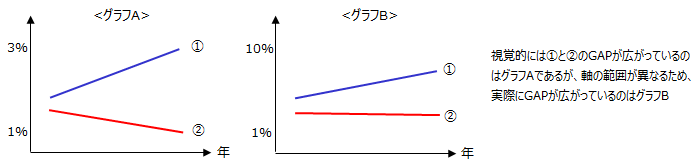
提示されたデータを分析する際に気を付ける事の最も初歩的な事の一つに、軸情報がどうなっているかを確認する必要があります。以下はある特性の広がりを比較したグラフですが、一見するとグラフBよりグラフAの①と②のGAPが広がっている様に見えますが、縦軸の目盛りが異なるため、実際にGAPが広がっているのはグラフBとなります。

グラフを視覚的に見やすくしたいという気持ちで初心者はついやってしまうミスですが、見る人に誤った判断をさせるために意図的に行う人もいるので、見る人は十分気を付ける必要があります。また軸の単位に値の絶対値で示されている場合も気を付ける必要があり、母数に対する比率はどうなのかも考慮しましょう。

軸の幅や単位の問題は、データ自体に嘘はないので100歩譲って認める事ができたとしても、以下の様な円グラフは、数値が正しいとしたらデータそのものを加工しなければこの円グラフの形は実現できないので、問題のレベルは大きいです。

＜人の特性を知る＞
データを見る人間の特性についても理解しておく必要があります。人は数値だけのデータで説明されるより、グラフを見せられた方が納得しやすいという特性を持っています。確かに自分自身にも当てはまっていると思います。グラフを見ると何となく信ぴょう性が高まった気がしますが、安易に信じたりせずに、「それは何故なのか」という疑問を持つことが大切です。

サブチャンネルあります。⇒ 何かのお役に立てればと