MAP推定法,最尤推定法とは

■MAP(MAximum a Posteriori)推定
MAP推定とは最大事後確率推定ともいい、事後分布が最大な点がその事象が発生する真の確率とする考えです。

具体的な例で考えます。オモテの出る確率がθのコインがある。このコインを3回投げた時、オモテ、オモテ、ウラの順で出た。この時オモテの出る確率θの確率分布は以下のとおり。詳細な計算方法はこちらで説明しております。

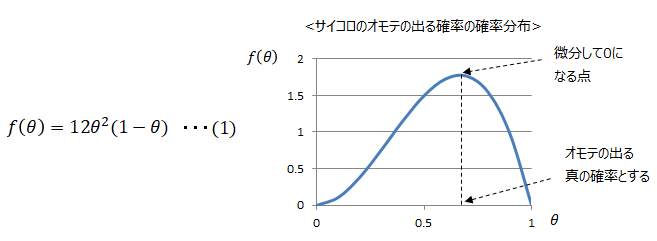
上図に示すように、f(θ)が最大になる点がオモテの出る真の確率の推定値となります。実際に計算してみます。上式を微分してその解が0になるθの値を求めます。

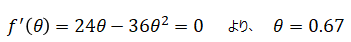
となり、真のオモテの出る確率の推定値を求めることが出来ました。

■最尤推定法(MLE:Maximum Likelihood Estimation)
最尤推定法もMAP推定と同じく、その事象が発生する尤もらしい確率を求める手法となります。具体例は先ほどと同じく、コインがオモテ、オモテ、ウラと出た時、オモテの出る確率を求めるというものです。

オモテの出る確率をθ、ウラの出る確率を1-θとするとき、

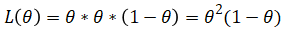
となります。L(θ)を尤度関数といいます。

上式を見てわかる様に、MAP推定で求めた(1)式と形がほぼ同じになっているのが解ります。微分の結果は同じになるので、グラフで表しても当然ながら最尤値は同じです。

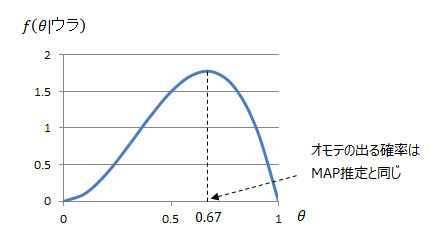
■MAP推定と最尤推定法の違い
上記の結果から解るとおり、両者から求められる結果は同じく、式の形もほとんど同じになります。違いは、MAP推定は面積の総和が1になるという特徴を持っているという点で、最尤推定法で求めた尤度関数を正規化したものが MAP推定と考えることが出来ます。