確率分布のベイズ推定(正規分布に従う場合)

こちらで確率分布のベイズ推定方法について説明しましたが、追加で例題を考えます。

■例題
内容量100gと表示された製品の、実際の内容量xは正規分布に従い、分散は1であることが分かっている。製品を1つ抽出し調べたところ内容量は90gであった。このとき製品内容量の「平均値μの確率分布」を求めよ。

■回答
まず、確率分布のベイズ推定式は以下となります。

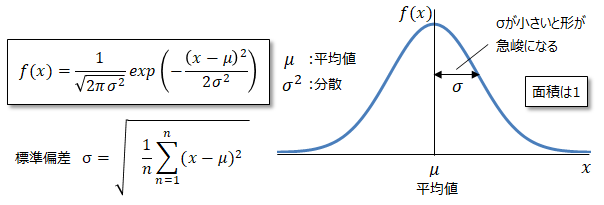
また計算に必要な正規分布は以下の形となります。

■事前分布
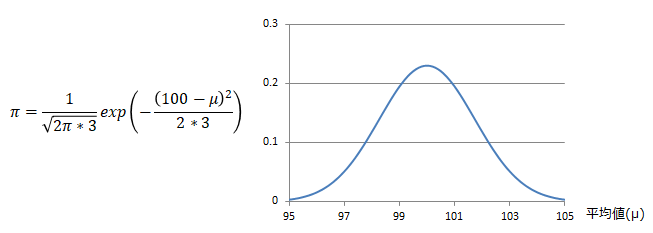
事前分布はとりあえず設定する(それで良いのがベイズ推定です)として、平均値は100を中心に分散が3の正規分布をしていると仮定します。なお、部品の重さの分散は1であると例題で定義しましたが、ここでは"平均値の分散"なので値が異なっても構いません。式とグラフは以下のとおり。

■尤度
得られたデータは正規分布に従うとした場合、尤度は以下の様に表されます。

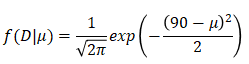
■事後分布
事前分布と尤度を掛け合わせると、

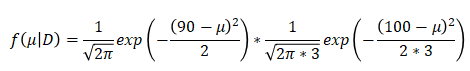
ここでe以外の部分は、上記式を積分した時に解が1になるような値が設定されるので、一旦無視して計算します。従って、

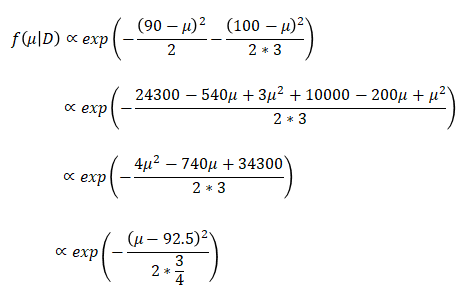
となり、中心値が92.5、分散が3/4の、平均値の確率分布となりました。この92.5が平均値が最大になる値としてMAP推定値となります(MAP推定値の説明はこちら)。また補正項は面積が1となるような値となります。以下積分の公式を使います。

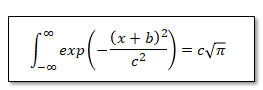
より、

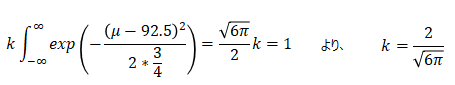
従って事後分布は以下となります。

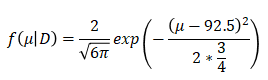
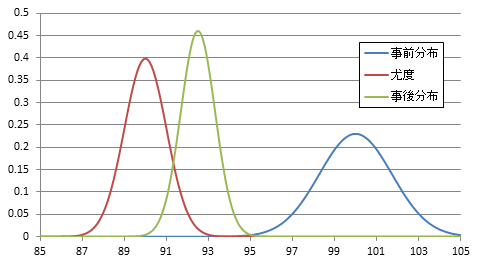
これまでの結果をまとめると以下になります。