公開日:2018/5/12 , 最終更新日:2024/1/28
前提知識python 乱数
■モンテカルロ法とは
モンテカルロ法(Monte Carlo method)とは乱数 を用いて数値計算を近似的に算出する方法のことです。
例えばサイコロの1の目が出る確率は理論上は1/6ですが、それをシミュレーションで何万回もサイコロを振って、その出た目から確率を求めると1/6に非常に近くなる。というものです。本当にそうなるか具体例で説明します。<pythonによる実装具体例①>
import numpy as np# 1~6までの値を10万個出力する # 1の出る確率 # 2の出る確率 # 3の出る確率 # 4の出る確率 # 5の出る確率 # 6の出る確率 ⇒ 0.1653
0.16735
0.16653
0.16817
0.16664
0.16601
<pythonによる実装具体例②>
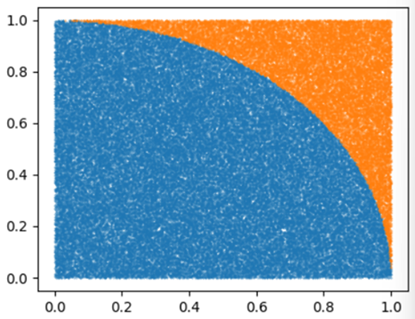
import numpy as np# サンプル数 # ランダムサンプル # 円の中の点 # 円の外の点 # 円の中の点の数 # 円周率
3.14176 となり、円周率を近似的に求めることができました(結果はその都度変わります)。プロット結果は以下のとおり。
サブチャンネルあります。⇒ 何かのお役に立てればと