|
前提知識
・単回帰分析、最小二乗法
・重回帰分析
こちらで重回帰分析の方法について説明しましたが、ここではエクセルによる回帰分析の方法を説明します。分析したいデータは以下とします。
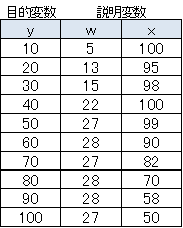
エクセルのツールバーから以下の様にクリックしていきます。
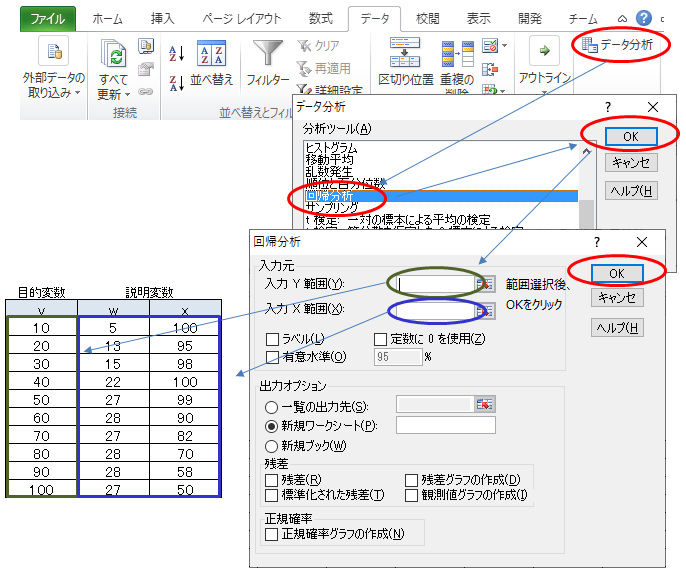
分析結果は以下となります。
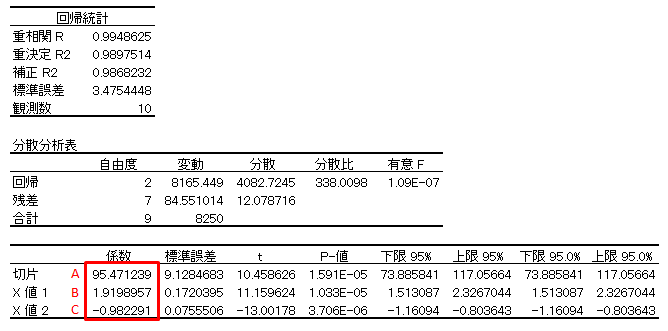
■分析結果の説明
まず一番重要なのは赤枠で囲った部分で、これが回帰式の係数となります。この場合回帰式は以下となります。
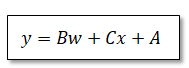
その他の項目が何を示しているかを説明します。
<重決定R2>
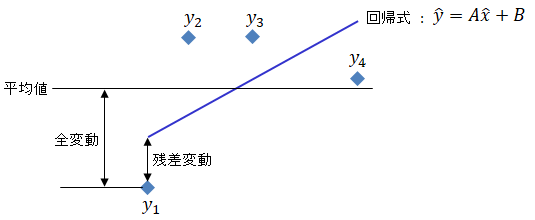
回帰式がどれくらい元のデータに近いかを表すもので、決定係数といいます。決定係数は以下の様に、全変動(全データの平均値と元データの差)に対する
残差変動(回帰式と元データの差)の割合を示したものになります。最大で1となり、1の時で元のデータと完全一致します。
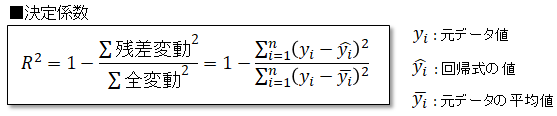
なぜR2か
R2とはRの二乗を意味しているのですが、そもそも決定係数は何故R2と表現するのでしょうか。これは分散の領域で出てくるのですが、二つのデータの相関関係を示す"相関係数"がrと表記しており、
それを2乗したら決定係数になる為、決定係数をR2と表現しています。相関係数の説明はこちら。では何故相関係数がrと表記するのか。
それはいろいろな説があり正しいことは不明です。
また注意する事として、相関係数を2乗したら決定係数になるのですが、決定係数は必ずしも相関係数を2乗したものではなく、
回帰式が実のデータと大きくかけ離れているとマイナスの値が出てくることもあります。
<重相関R>
上記でも説明した相関係数の事で、これを二乗すると決定係数になります。この係数が高い程、回帰式は実データをよく表現しています。
<補正R2>
自由度調整済み決定係数のことです。決定係数は説明変数を増やすだけ増加していく性質を持っていますが、
あまり効果のない説明変数であっても決定係数が大きくなってしまいます。そこでそれを補正するためのものが
自由度調整済み決定係数となり以下式で表します。
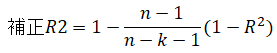
<有意F>
この値が小さい程回帰式の有効性を示しており、一般に0.05以下であれば有効であるとしております。
<P値>
説明変数が目的変数に対して効果がない場合、通常は回帰係数は0になると考えられますが、誤差によって0ではない値が出る場合があります。
その0ではない値がでる確率がP値となります。つまり値が小さい程、効果がないにもかかわらず係数に値を持っている確率が低く、係数が有効という事になります。
一般的に0.05以下であれば係数の有効性を認めることが出来ます。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|