確率過程とは

前提知識
　・確率変数
　・Scilabとは

確率過程とは、時間の経過など、ある条件に従って確率が変化する確率変数のことです。例えば、サイコロはどの目も1/6の確率で出るのが普通かと思いますが、 それが時間によって出る目の確率が変わる様なものです。確率過程の例を以下に説明します。

■ウィナー過程
ブラウン運動(液体中に浮遊する微粒子のランダムな運動)としてよく知られる確率過程で、正規性白色雑音(平均=0 , 標準偏差σ=1)を時系列で積分したものになります。式は以下。



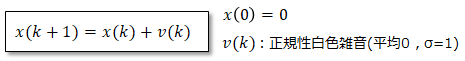
Scilabでのシミュレーション結果は以下のとおり。



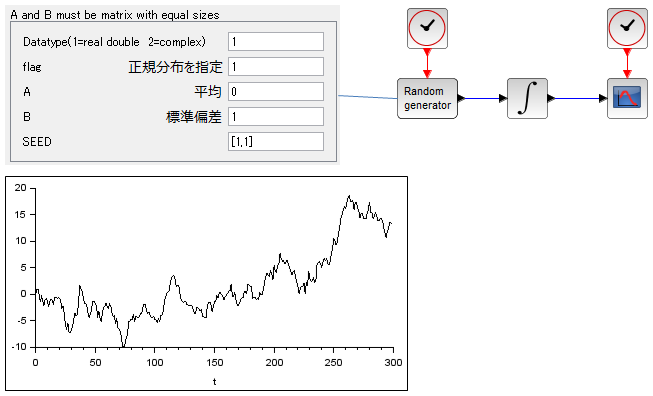
＜余談＞
上記グラフを見て株価の推移をイメージする人もいるかもしれません。バートン・マルキール著「ウォール街のランダム・ウォーカー」の中で、著者が友人の投資家にこのようなウィナー過程のグラフを見せたところ、 その投資家は「この会社はどこの会社だ？！今すぐ買うべきだ！」と言ったという。これはいかに株価が予測できないかという事を示しております。

■マルコフ過程
(N+1)回目の確率変数の値が(Ｎ)回目の確率変数の値のみから決まるものをマルコフ過程と言います。 これはベイズの定理を用いたベイジアンネットワークにも使われる考え方です。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 確率・統計 統計/解析 平均値、中央値、最頻値 平均値と期待値の違い 二乗平均、二乗和 移動平均 分散、標準偏差、共分散 偏差値 単回帰分析,最小二乗法 重回帰分析 リッジ回帰, ラッソ回帰 カーネル法, カーネル関数 ガウス過程回帰 エクセルによる回帰分析 最小二乗法の公式導出 主成分分析 疑似乱数, 準乱数 基底関数 仮説検定 モンテカルロ法 パレートの法則 データを正しく読む 有効サンプル数 ベイズ理論 ベイズの定理 ベイズの定理応用形 逐次ベイズ推定 ナイーブベイズフィルタとは 確率分布推定 確率分布推定(正規分布) MAP推定,最尤推定 ベイジアンネットワーク 確率 同時確率、条件付き確率 組み合わせの計算方法 確率変数 , 確率分布とは ・ベルヌーイ分布 ・二項分布 ・正規分布, ガウス分布 ・ポアソン分布 ・ベータ分布 ・ワイブル分布 ・カイ二乗分布 ・t分布 確率過程とは