主成分分析とは

■主成分分析とは
主成分分析(PCA:Principal Component Analysis)とは多変量解析手法の一つで、多くの変数によって説明されている対象物の特性に対して、その特性を最も特徴づけている変数が何かを分析する手法です。

主成分分析の活用例として、例えばAさんとBさんのテストの点数が以下だった時、どちらのほうが学力の総合力が上と見るでしょうか？合計点が高いAさんのほうが上でしょうか？

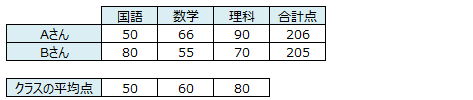
主成分分析の考えに従うと、平均点(正しくは分散を使用)が低い英語で高い得点を得ている、Bさんの方が総合力があると考えます。この考え方は直感的に納得できるかと思いますが、定量的に表す必要があります。英語の点数に何かしらの重み付けて各点数を合計すればよいのですが、具体的には分散が最大なるような新しい変量を作成し、それの合成変量を求めればよいです。なお上記の合計点は、各変量を単純に加えた合成変量と言えます。

■主成分分析の考え方

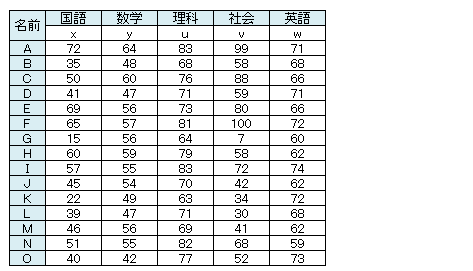
＜第1主成分の抽出＞
上記を例に生徒のテスト結果に対して主成分分析を行います。以下式のとおり、合成変量pが最大の分散値を持つような係数(a,b,c,d,e)を求めます。この時pを主成分、係数を主成分負荷量と言います。係数はラグランジュの未定乗数法を用いて求めますが、エクセルのソルバーという機能を用いると簡単に求めることができます。

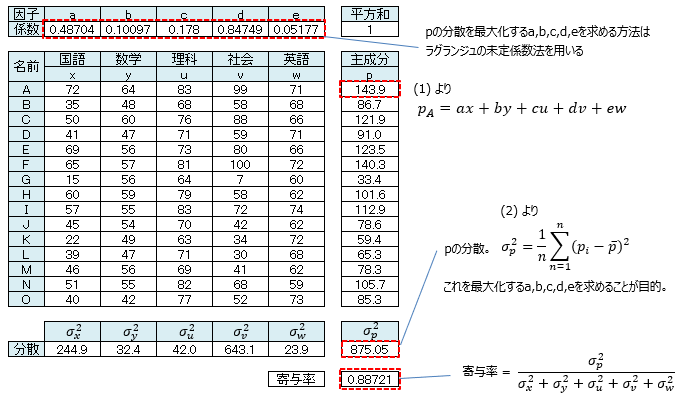
第1主成分の解釈
　・係数が最も大きな「社会」がこのデータを最も特徴づける変数である
　・主成分pは、係数を考慮した5科目の総合力であり、Aさんが最も総合力が高い

また今回生成した合成変量が、全体のデータに対してどれだけ個々の特性を取り込んでいるかを表す指標に寄与率があり(式は上記参照)、今回約89%の寄与率であることが分かりました。

＜第2主成分の抽出＞
全体のデータから第1主成分を除いた状態で、もう一度主成分分析を行ったものを第2主成分といいます。この第2主成分の抽出まで行う場合が多いようです。第2主成分抽出用の変量は以下式で定義します。

先ほどと同様の計算をすると、第２主成分が求まります。

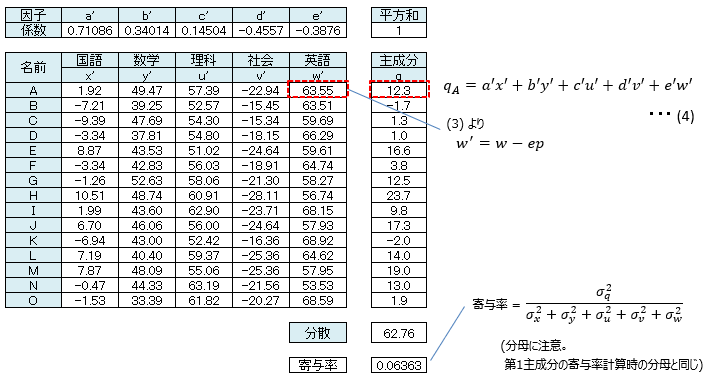
なお、(4)式に(3)を代入すると以下となる。

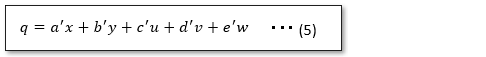
第2主成分の解釈
　・社会の次に「数学」がこのデータを最も特徴づける変数である
　・係数がプラス同士の科目、マイナス同士の科目が、それぞれ得意不得意の傾向が似ている

また、第1主成分と第2主成分の寄与率を足したものを累積寄与率といいます。

サブチャンネルあります。⇒ 何かのお役に立てればと