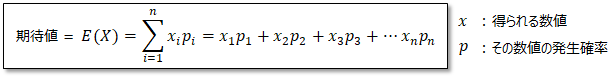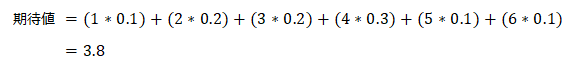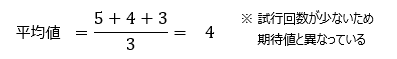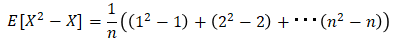平均値と期待値の違い

・In English
前提知識
・平均値

■期待値

期待値とは、ある試行の結果として得られるであろう数値の平均値のことであり、例えば宝くじで得られる金額の平均値や、サイコロの出る目の平均値等が期待値で表す事ができます。式は以下。



例えば、サイコロの出る目の確率が以下の時、サイコロの出る目の期待値を求めます。



計算式は以下。

■期待値と平均値との違い

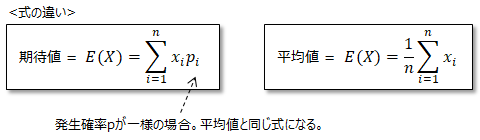
上記で説明したとおり、期待値は平均値の一種です。違いは、期待値はこれから行う試行に対して予測される平均値で、既に試行した結果に対しては平均値といいます。 また、期待値のp(発生確率)が一様の場合、期待値の式は平均値と同じになります。



両者の違いをサイコロを例に説明すると、サイコロを振る前でも理論値として解るサイコロの出る目の平均値が期待値で、実際にサイコロを振って出た目から算出する場合は平均値として扱います。 サイコロを振る回数を多くすればするほど平均値は期待値に収束します。

<例>
期待値が上記(1)に従うサイコロを3回振って出た目が5,4,3だった。サイコロの出た目の平均値は？

■期待値の罠

例えば、90%の確率で1000万円当たるクジと、10%の確率で1億円当たるクジ、1度だけどちらを選ぶかという状況があった場合、 「期待値が高い1億円のクジを選ぶ」と考える人がいるかもしれませんが、期待値での比較が有効なのは試行回数が多い場合なので、一回の試行において期待値で損得を比較するのは得策ではありません。 この場合、理論的にどちらを選ぶのが正しいという答えはないですが、人間の行動心理として損失回避願望が働き、金額は少なくても貰える可能性の高い1000万円のクジを選ぶ人が多いようです。 裏を返せば、数値に惑わされず、より心理的なダメージが少ない方を選ぶのが得策といえるかもしれません。

■期待値の記号

期待値は上記で示したとおりEで表すことができます(EはExpectationの意味)が、以下の様にEの中に多項式を入れて、その多項式の期待値(または平均値)を算出する事が良くあります。 例えば分散を求める場合など。



なお、平均値は以下エックスバーで表すことができます。しばしばEと同義でエックスバーを用いります。



また母平均はμ(ミュー)で表します。上記の場合、xは標本データの平均であるため、母集団の平均を表しているとは限りません。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 確率・統計 統計/解析 平均値、中央値、最頻値 平均値と期待値の違い 二乗平均、二乗和 移動平均 分散、標準偏差、共分散 偏差値 単回帰分析,最小二乗法 重回帰分析 リッジ回帰, ラッソ回帰 カーネル法, カーネル関数 ガウス過程回帰 エクセルによる回帰分析 最小二乗法の公式導出 主成分分析 疑似乱数, 準乱数 基底関数 仮説検定 モンテカルロ法 パレートの法則 データを正しく読む 有効サンプル数 ベイズ理論 ベイズの定理 ベイズの定理応用形 逐次ベイズ推定 ナイーブベイズフィルタとは 確率分布推定 確率分布推定(正規分布) MAP推定,最尤推定 ベイジアンネットワーク 確率 同時確率、条件付き確率 組み合わせの計算方法 確率変数 , 確率分布とは ・ベルヌーイ分布 ・二項分布 ・正規分布, ガウス分布 ・ポアソン分布 ・ベータ分布 ・ワイブル分布 ・カイ二乗分布 ・t分布 確率過程とは