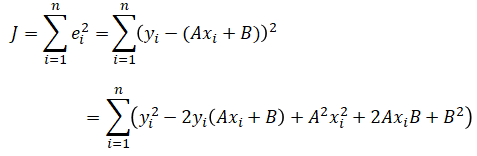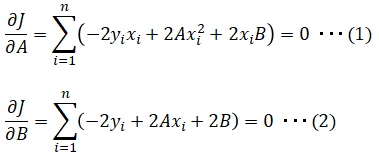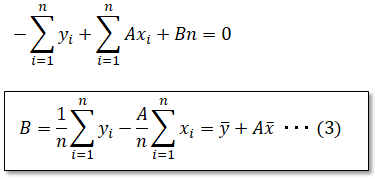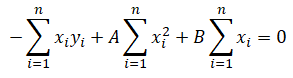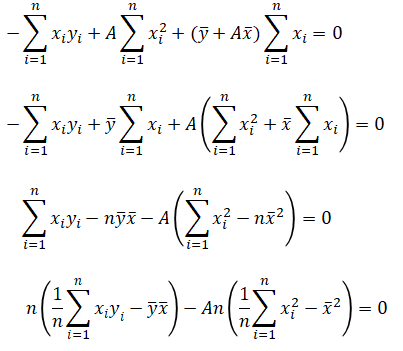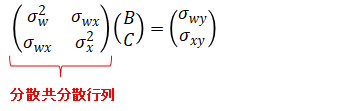最小二乗法の公式の導出方法

　・In English
前提知識
　・分散、共分散とは
　・最小二乗法とは

■最小二乗法による単回帰式の導出方法

こちらでも説明した様に、最小二乗法によって求める単回帰式は以下ですが、その導出方法を説明します。



先ず最小二乗法は回帰式との残差の平方和が最小となる様なAとBを求めるので、以下のとおりとなります。



上式をAとBで偏微分します。



(2)式を以下のとおり変形。簡単化のため各項を2で割っています。



となり、Bを求めることが出来ました。y_i, x_iの積算をnで割ることは平均を意味しているのがポイントです。

次に(1)を以下のとおり変形。こちらも各項を2で割っております。



(3)を上式に代入



となります。分散の公式より、



より、



となり、Aも求めることができました。

■最小二乗法による重回帰(2変数)式の導出方法

説明変数が2変数(w , x)の場合の公式は以下となります。導出方法の考え方は単回帰の時と同じなので、詳細な計算過程は省略します。



なお(4)式はまとめて以下の様に行列で表現すると解りやすく、この行列を分散共分散行列と言います。

■最小二乗法による重回帰(3変数)式の導出方法

以下となります。変数が増えても同じように対応が可能です。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 確率・統計 統計/解析 平均値、中央値、最頻値 平均値と期待値の違い 二乗平均、二乗和 移動平均 分散、標準偏差、共分散 偏差値 単回帰分析,最小二乗法 重回帰分析 リッジ回帰, ラッソ回帰 カーネル法, カーネル関数 ガウス過程回帰 エクセルによる回帰分析 最小二乗法の公式導出 主成分分析 疑似乱数, 準乱数 基底関数 仮説検定 モンテカルロ法 パレートの法則 データを正しく読む 有効サンプル数 ベイズ理論 ベイズの定理 ベイズの定理応用形 逐次ベイズ推定 ナイーブベイズフィルタとは 確率分布推定 確率分布推定(正規分布) MAP推定,最尤推定 ベイジアンネットワーク 確率 同時確率、条件付き確率 組み合わせの計算方法 確率変数 , 確率分布とは ・ベルヌーイ分布 ・二項分布 ・正規分布, ガウス分布 ・ポアソン分布 ・ベータ分布 ・ワイブル分布 ・カイ二乗分布 ・t分布 確率過程とは