平均値、中央値、最頻値の使い方

具体例としてテストの点数が以下の時の、各代表値の求め方を説明します。

■平均値
データの数値の合計に対して、データの個数で割った値です。

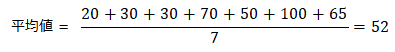
長所：全てのデータを反映させることができる
短所：極端に大きな/小さな値に左右される。例えば、一部の年収の高い人に引きずられ年収の平均値が上がる。

なお平均値の計算を一般式で表すと以下となります。やっていることは非常に単純なのに、一般式で表すと非常に難しい事をやっている様に感じます。

■中央値 (メジアン)
データを小さい(大きい)順から並べた時にちょうど中間に位置するデータです。データの個数が偶数個の場合は中間の二つの値の平均です。

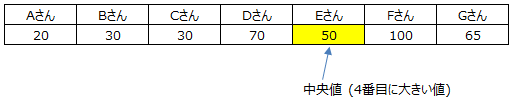
長所：極端な値があっても平均値の様には影響を受けづらい。
短所：端の意味あるデータを無視してしまう。例えば以下の様に、次のテストでみんな努力して点数が上がったのにもかかわらず、中央値としては変わらない値になっています。これは狙いの結果ではないことが解ります。

■最頻値 (モード)
最も出現率の高いデータです。

長所：中央値同様に外れ値の影響を受けづらい。中央値よりも実感に合う場合がある。
短所：データ数が少ない場合や、まんべんなくデータが分布している場合、ごく一部のピークを捉えてしまう場合がある。ただし、多数決で代表値を決めてしまいたい場合に使うのはあり。

■トリム平均値
上下一定数を除いた残りの平均値

長所：平均値と中央値の長所を併せ持つ
短所：どこまでの値を除去するかで結果が異なる。結果が作為的なものになる可能性がある。

＜どの代表値を使えば良いか＞
データの特性に合わせ適切な代表値を用いる必要がありますが、一つの考えとして、データの分布が正規分布に近い場合は平均値を用いた方が良いと思われます。正規分布とは異なり外れ値がある場合は、平均値以外を使う事を検討した方が良いです。

サブチャンネルあります。⇒ 何かのお役に立てればと