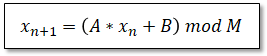疑似乱数とは, 準乱数との違い, pythonの実装例

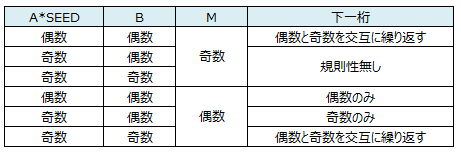
疑似乱数とは、乱数列に見えるが実際には特定のアルゴリズムによって決まっている数列の事です。コンピュータで生成される乱数はほとんどが疑似乱数です。完全な乱数を作ろうと思ったら、例えば多面体のサイコロを実際に振って出た目の数値を扱うとか、コンピュータに接続されたデバイスからの入力のノイズ情報を扱う等、コンピュータ外からの入力を用いれば実現できますが簡単ではありません。下記に述べる「シード」は外部情報を用いて設定できますが、それでも一定のアルゴリズムに従っているというのが前提にあります。

なおシミュレーションを行う上では、再現性のある乱数というのも求められるので、完全な乱数よりも逆に疑似乱数の方が良い場合もあります。ちなみに、テレビゲーム等においては、アイテムの発生条件や、敵とのエンカウントに疑似乱数を使っている事が多く、疑似乱数の再現性の性質を利用(悪用？)して狙いのアイテムを得る等の裏技が使われる場合があります。これを乱数調整と言います。

疑似乱数生成の考え方、生成アルゴリズム例を以下に示します。

＜線形合同法＞

疑似乱数生成を理解するのには最も手頃な手法で、これまで広く使われていた手法です。式は以下漸化式となります。

modはカッコの中の数字をMで割った余りを意味します。従って乱数の範囲はMより小さい値となります。またx_nの初期値x₀をSEED(シード)といいます。プログラムの関数でユーザーがシードを設定しない場合は、現在の時刻から決めた値などをデフォルトで設定したりします。

この手法の欠点は、以下のように値の設定すると下一桁に規則性が出てくることで、特にMを偶数に設定した時は、奇数と偶数が交互に出たり、必ず奇数もしくは偶数になります。

この欠点が致命的となった有名な例として、Xbox向けの「カルドセプトサーガ」というボードゲームのダイスの出る目が、偶数と奇数を交互に出してしまうというバグがありました。

＜Mersenne-Twister(メルセンヌ・ツイスター)＞

日本人が考えたメルセンヌ素数を用いたアルゴリズムで、高いランダム性と周期性が実現でき且つ計算速度が速いことから、非常に高い評価を得られており、pythonやMATLAB、C++などでデフォルトの乱数発生器として用いられています。最大周期が2¹⁹⁹³⁷-1の時、MT19939と呼ばれます。

なおメルセンヌ・ツイスターは高いランダム性を持っていますが、それでもアルゴリズムで生成されており値を読み解くことができるため、メルセンヌ・ツイスターといえども暗号には使用できません。

＜xorshift＞

排他的論理和(XOR)とビットシフトを用いた演算で、比較的長周期(2¹²⁸-1)の乱数を生成できる割に計算が高速である。

■準乱数とは

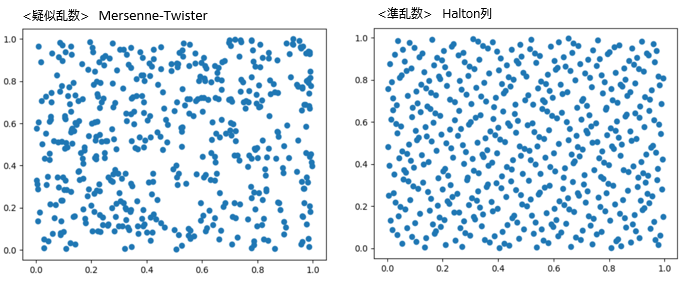
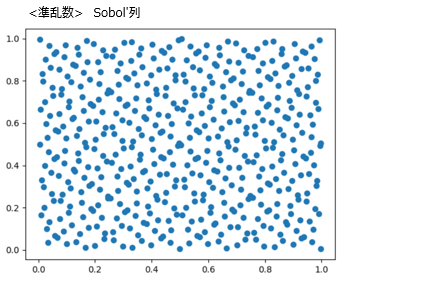
準乱数とは、空間上に一様に配列されるようにした乱数です。疑似乱数は局所的には値の偏りを持ってしまう(それが真の乱数に近い証拠)ため、偏りを小さくしながらできるだけランダムにしているのが準乱数です。以下が疑似乱数と準乱数の比較です。

■疑似乱数と準乱数のpython実装例

上記グラフを描画するプログラムは以下のとおりです。

import numpy as np
import matplotlib.pyplot as plt
import chaospy as cp

a = np.random.rand(2,500) # 疑似乱数:Mersenne-Twister
b = cp.create_halton_samples(500, 2) # 準乱数:Halton列
#b = cp.create_sobol_samples(500, 2) # 準乱数:Sobol'列

plt.figure()
plt.plot(a[0], a[1], 'o')
plt.figure()
plt.plot(b[0], b[1], 'o')
plt.show()

なお、上記プログラムのHlton列をsobol'列に入れ替えた場合、結果は以下のとおりになります。

サブチャンネルあります。⇒ 何かのお役に立てればと