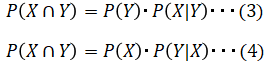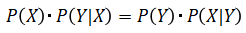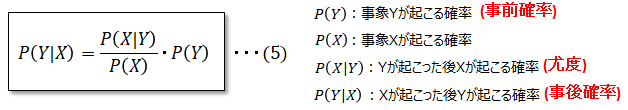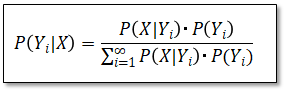|
| 公開日:2018/1/9 , 最終更新日:2018/2/28
|
前提知識
・条件付き確率
■ベイズ理論の考えかた
以下問題を例にベイズ理論の考え方について考えてみます。
<例題>
これまでサイコロを4回連続で振って全て1が出た。次に5回目のサイコロを振るとき、1が出る確率は?
① 5回連続で1が出るのはまずありえない。確率は1/6より低い。
② サイコロを振るのは独立した事象なので、前の結果がどうであろうと1/6である。
③ 前に4回も連続して1が出るという事は、1が出やすいサイコロの筈なので確率は1/6より高い。
これまでの考えでは②となるかと思いますが、ベイズ理論の考えに従うと③が正解となります。これはどういう事かというと、
まさに例題にある様に、事前に1がたくさん出ているのでこれは1が出やすいサイコロだと考え、確率を1/6より高く見積もるというものです。
つまりベイズ理論の考え方とは、事前に起きた事象を踏まえ次の発生する事象の確率を精度よく求めるというものです。
従来の考えを頻度論といい、サイコロの発生する確率はただ一つであるべきで、それこそサイコロをたくさん振って得られた結果から確率を求めるというものです。
一方ベイズ理論の考えは、確率は試行の過程を経て求めていき最終的な確率に近づけていくという考えです。
■ベイズの定理導出
ベイズ理論の基本となる、ベイズの定理の導出方法を説明します。ベイズの定理とは条件付き確率を応用した考えになります。
まず条件付き確率とは以下で表現し、これはYという条件が起こった前提でXが起こる確率 P(X|Y)を表してしております。
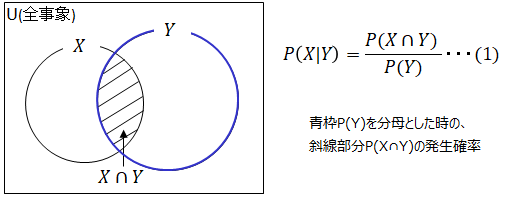
一方で、Xが起こった前提でYが起こる確率 P(Y|X)は以下の様に表せます。
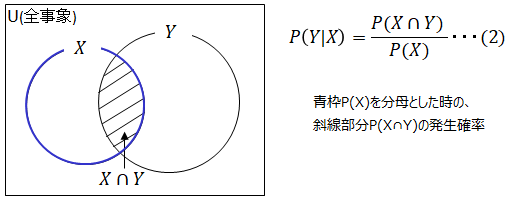
(1)(2)式は以下の様に変形できます。これを乗法定理と言います。
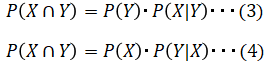
上記より、
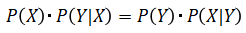
よって、以下がベイズの定理となります。
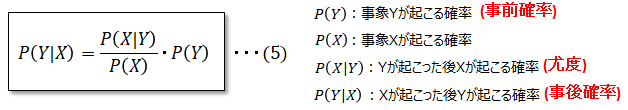
この式が意味するのは、もともとYが発生する確率(事前確率)はP(Y)であったが、その後Xが発生する確率(尤度) P(X|Y)という新しい情報を得たことで、
Yの発生する確率(事後確率) P(Y|X)を精度よく求めることが出来るというものです。
また(5)式は次の様にも変形できます。詳細説明はこちらを参照。
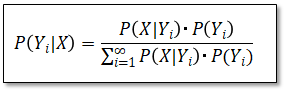
■例題:モンティホール問題
ベイズの定理を使って有名なモンティホール問題を考えてみます。モンティホール問題とはアメリカのクイズ番組で取り上げられたクイズに対して
その真偽をめぐった論争のこと、もしくはそのクイズのことです(モンティとはその番組の司会者の名前)。クイズの内容は以下。
① 3つのドアがある。1つだけ当たりで、二つはハズレ。
② 挑戦者は3つの中から一つのドアを選択する。
③ モンティはどれが当たりか知っており、残りの2つのドアの中でハズレの一つを開けて見せる。
④ この時点で挑戦者は残りのドアに選択を変えることが出来る。変えるべきか、変えないべきか?
ベイズの定理を使わずに考える
挑戦者がドアを選択(Aを選択したと仮定します)した時点では、どれも当たる確率は同じ1/3です。
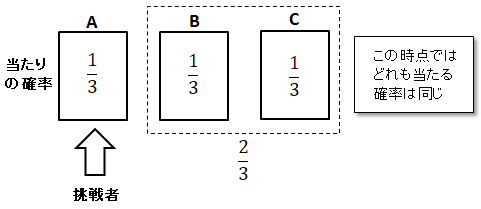
しかしモンティが、挑戦者が選ばなかった残りの二つのうちハズレの一つ(Bと仮定)を開けてしまうとどうでしょうか?
残りの一つ(C)に当たりの確率の2/3が集約されることになります。
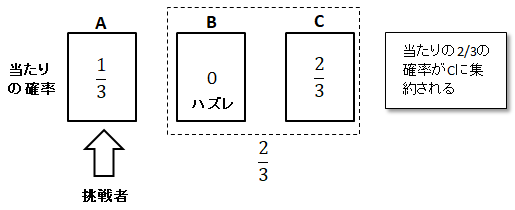
つまりCが当たる確率が最も高くなるので、挑戦者はCに変えた方が良いという事になります。
ベイズの定理を使って考える
ベイズの定理で求める確率は以下2つになります。
① 挑戦者がAをした状態でドアBを開いた後に、ドアAが当たりとなる確率:P(A|B)
② 挑戦者がAをした状態でドアBを開いた後に、ドアCが当たりとなる確率:P(C|B)
まず① ドアBを開いた後に、ドアAが当たりとなる確率:P(A|B)を求めます。

となります。
次に、② ドアBを開いた後に、ドアCが当たりとなる確率:P(C|B)を求めます。

となり、ベイズの定理からもCに変えた方が良いという事が解ります。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|