確率変数、確率分布、確率密度関数とは

■確率変数、確率分布
サイコロの目の様に、確率的に値の決まる変数を確率変数といいます。例えばサイコロの目だと1,2,3,4,5,6が確率変数となり、またコインを投げた時に、オモテを1ウラを0としたときに、1,0が確率変数となります。

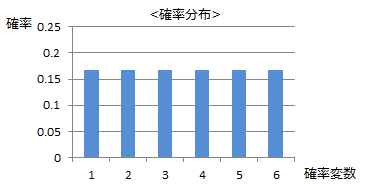
確率変数の取りうる値に対して、それぞれの発生する確率を表した分布を確率分布といいます。例えばサイコロの目の確率変数に対する確率分布は以下となります。確率分布の表すそれぞれの確率を尤度といいます。

■確率密度関数
確率変数がサイコロやコインの様な離散的な確率分布を取るものに対し、身長の分布の様に連続的な確率分布を取るものに対しては 確率密度関数というもので表現すると便利です。以下の様に表現できます。

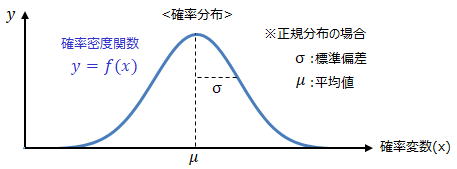
また分布を特徴づける数を母数もしくはパラメータといいます。上記は正規分布の確率分布なのですが、正規分布においては平均値や分散が母数となります。母数とは分母とは別物ですが誤用される場合がありますので注意が必要です。パラメータといった方が直感に合うような気がします。

確率密度関数の性質
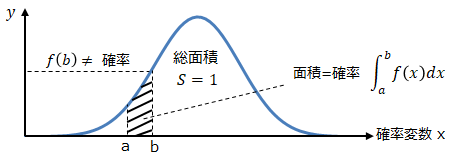
確率密度関数は連続的な値を取る場合、xを関数y(x)に代入してもその解がxの確率とはなりません※。確率を求めるには所定範囲内のX軸と挟まれた領域の面積を求める必要があります。なおy(x)の総面積は1となります。

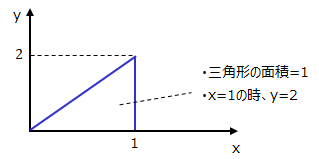
※なぜ連続系の場合は、xを関数y(x)に代入してもその解がxの確率とはならないのか。例えば以下三角形の密度関数があったとします。三角形の面積は1なのに、x=1の時のy(x)は2となり、y(x)が確率となるなら、三角形の面積より大きくなり矛盾してしまいます。離散系の確率分布の場合は、x値のyがそのまま確率となります。