カイ二乗分布とは　その意味と用途

・In English
前提知識
　・確率分布
　・標準正規分布
　・ガンマ関数

■カイ二乗分布とは

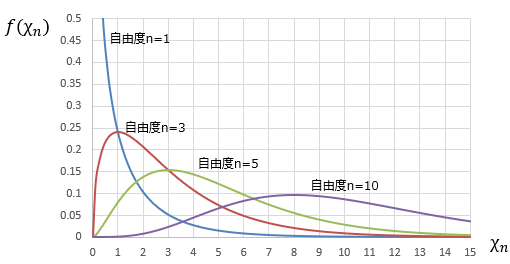
カイ二乗分布とは、平均値0、分散1の標準正規分布に従うn個の確率変数Z₁, Z₂,・・・Z_nをサンプルした時、 以下の様に確率変数の二乗和で表されるχ(カイ)の確率分布のことです。このときサンプル数nを自由度といいます。また、Γはガンマ関数といいます。



グラフに表すと以下のとおり。

■カイ二乗分布の意味

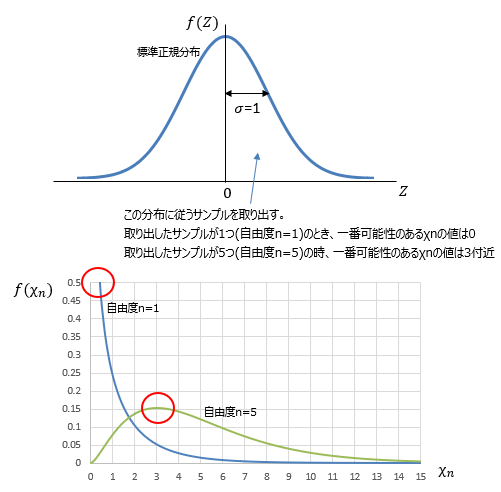
例えば以下の様に、標準正規分布に従うサンプルを1つだけ取り出した時(自由度n=1の時)、そのサンプルが取りうる値で最も可能性が高い値は「0」になります。 つまり、χ_n=0が最も可能性が高いので、その時のf(χ_n)が値が最も大きくなります。

またサンプルを3つ取り出した時(自由度n=3の時)、そのサンプルは全て0付近の値をとる訳ではないので、χ_nは0より大きくなることが想像できます。 ではどの辺りの値が最も可能性が高くなるかというと、3付近が最も可能性が高くなるという事を意味しています。

■カイ二乗分布の用途

サンプルを複数個取り出した時のχ_nを計測することで、そのサンプルが本当に標準正規分布に従っているサンプルなのかを検査することができます。 もしχ_nが理論値から大きく外れていたら、そのサンプルは規格外の部品であるという事が分かります。これをカイ二乗検定といいます。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 確率・統計 統計/解析 平均値、中央値、最頻値 平均値と期待値の違い 二乗平均、二乗和 移動平均 分散、標準偏差、共分散 偏差値 単回帰分析,最小二乗法 重回帰分析 リッジ回帰, ラッソ回帰 カーネル法, カーネル関数 ガウス過程回帰 エクセルによる回帰分析 最小二乗法の公式導出 主成分分析 疑似乱数, 準乱数 基底関数 仮説検定 モンテカルロ法 パレートの法則 データを正しく読む 有効サンプル数 ベイズ理論 ベイズの定理 ベイズの定理応用形 逐次ベイズ推定 ナイーブベイズフィルタとは 確率分布推定 確率分布推定(正規分布) MAP推定,最尤推定 ベイジアンネットワーク 確率 同時確率、条件付き確率 組み合わせの計算方法 確率変数 , 確率分布とは ・ベルヌーイ分布 ・二項分布 ・正規分布, ガウス分布 ・ポアソン分布 ・ベータ分布 ・ワイブル分布 ・カイ二乗分布 ・t分布 確率過程とは