|
前提知識
・ベイズの定理
こちらでベイズの定理を説明しましたが、その定理の応用形を説明します。ベイズの定理は以下でした。
これは「Xという事象が起こった前提でYが起こる確率」を意味しております。
■ベイズの定理
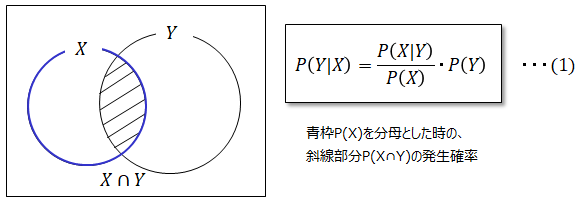
上記ベン図を解りやすく説明するため以下の様に変形します。
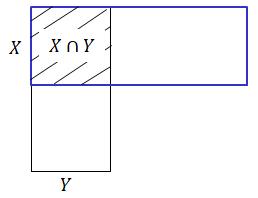
Xを別の方法で表現します。Xと同時に発生する事象は以下の様に複数あり、Xの全事象を説明できると考えます。
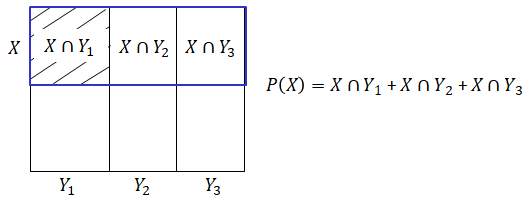
これを全確率の法則といい、一般化すると以下式となります。
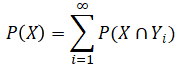
こちらで説明したとおり、
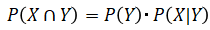
より、
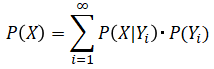
これを(1)式に代入すると以下のベイズの定理の応用形となり、これも重要な公式となります。
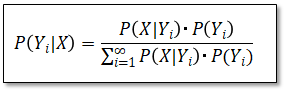
■例題
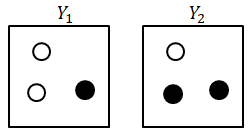
箱が二つありこれをY1、Y2と付けます。Y1の中には白い玉が二つ、黒い玉が1つ、Y2の中には白い玉が一つ、黒い玉が2つ入っています。
これを目隠しでどちらかの箱の中から一つ玉を取り出したところ、黒い玉だった。これがY2の箱から取り出した確率は?ただしY1とY2の選ばれる確率はそれぞれ3対1である。
■回答
式は以下となります。
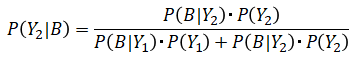
これを一つ一つ考えていくと、

上式に代入すると、

となります。これで最初の確率(事前確率)より、黒を引いたという情報を得た場合の確率(事後確率)の方が確率が上がり、精度が良くなっている事が分かります。
■理由不十分の法則
上記の例題では、箱を取り出す確率というのが定義されていました。しかし、箱を取り出す確率というのが解らない場合もあります。
その場合ベイズ理論では、「何も情報が無ければ確率は同等」という考えを用います。これを理由不十分の原則といいます。
これはベイズ理論が主観確率を用いているとよばれる理由の一つともなります。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|