二項分布とは

こちらで説明した様に、「コインを投げてオモテが出るかウラが出るか」の様に、結果が2パターンにしかならない試行をベルヌーイ試行といいますが、このベルヌーイ試行をn回実施しどちらか(例えばオモテ)が出る回数の確率分布を二項分布といいます。

ここでオモテの出る確率をP、ウラの出る確率を1-Pとしたとき、このコインをn回投げてオモテがk回出る確率は以下の様に表します。組み合わせ(nCr)の計算についてはこちらを参照。

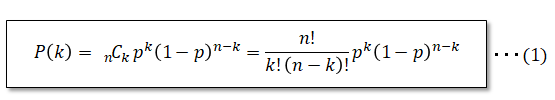
例えば、オモテの出る確率P=0.6のとき、コインを5回投げてオモテが3回出る確率は以下。

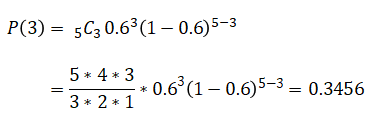
オモテの出る回数に対する確率を以下の様にまとめます。確率の合計は当然ながら1になります。

グラフにすると以下。

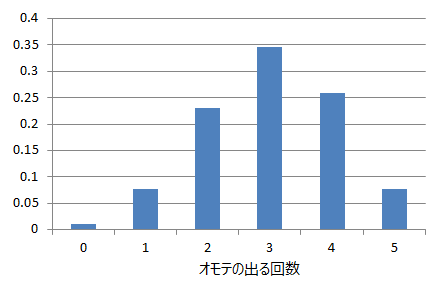
■二項分布の特性
試行数nを大きくすると、二項分布は正規分布に近づきます。n=100とした時の結果は以下。

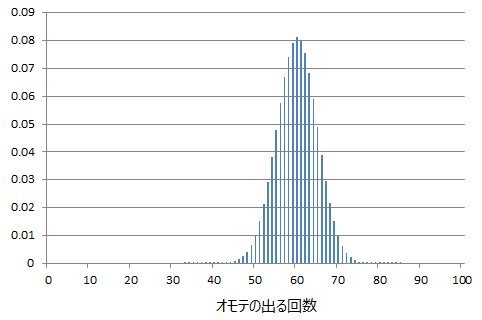
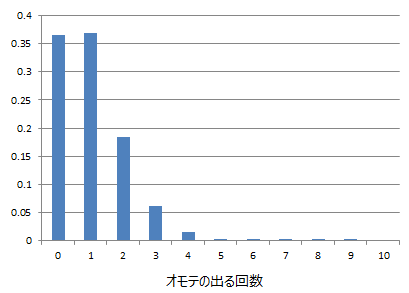
更にオモテの出る確率pが非常に小さい場合、分布はポアソン分布になります。p=0.01、n=100としたときの分布は以下。

■二項分布の極限がポアソン分布になる証明
先ずポアソン分布は以下となります。ここで単位間隔での平均発生回数をλ、その中で単位間隔に発生する回数をkとします。 (1)式においてn=∞時に以下になる事を証明します。

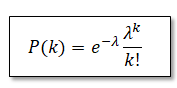
(1)式を以下の様に変形。

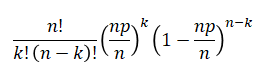
ここでnpは平均発生回数λとなりますので、np=λとおき、更に式変形すると、

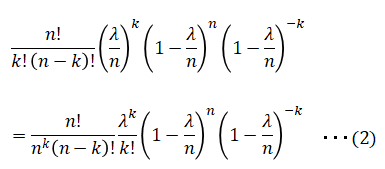
ここでn=∞とすると、

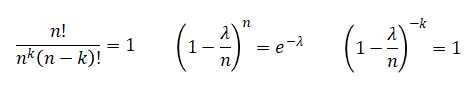
となり、(2)に代入すると、

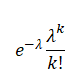
となり、ポアソン分布の形になる事が証明できました。