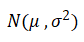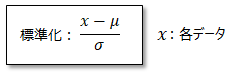正規分布, ガウス分布とは　標準化と正規化の違い

前提知識
　・標準偏差
　・ガウス関数の積分方法

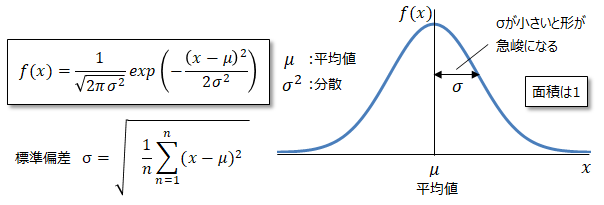
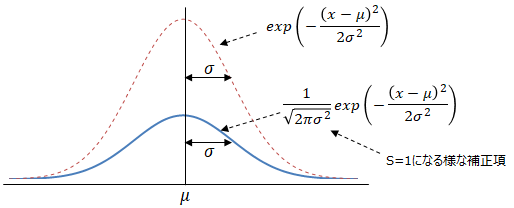
■正規分布(Nomal distribution)とは

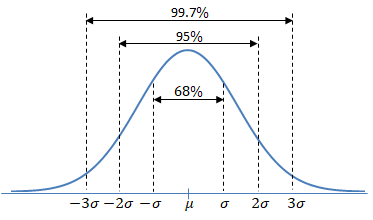
正規分布とは、自然界における最も標準的(Normal)な分布といわれており、以下特性を持った確率分布となり。 例えば、10歳男児の身長の分布、テストの点数の分布、ボルトの長さの分布など、正規分布で表されると考えられてます。ガウス分布またはベルシェイプ(釣鐘型)などとも言います。

　①平均値と最頻値と中央値が一致し、そこが最も確率が高い。
　②平均値から左右対象に広がっていく。
　③分散が大きくなると山の形は低く、なだらかとなる。

確率密度関数は以下。σ(シグマ)は標準偏差といい分布のバラツキ具合を表すために用います。μは平均値、σの二乗が分散で、 μ=0、σ=1のときの分布を標準正規分布といいます。



なお正規分布を以下の様にも表現します。


また所定区間内の面積比率(データ存在確率)は以下の様になっており、例えば1σ内だと68%となります。



＜補足＞
確率密度関数の指数部分ではない項は、面積の総和が1にするための補正項となります(詳細はこちら)。 従って分布の形を決定する要素(平均値、分散)は変わらないのでグラフの形は相似形になります。

■標準化(standardization)とは

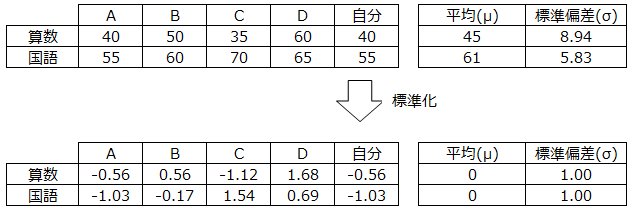
正規分布に従うデータを、標準正規分布に従うデータに変換する事を標準化といい、以下式で表します。



標準化する事で、異なるμ、σをもつ母集団の特性を比較するのを容易にします。例えば、以下の様に自分の算数と国語のテストの点数が どちらが良い結果であるかを知るときは標準化すると便利です。



上記のとおり、算数の方が分布のより右側にいるので、算数の方が良い点であることが解ります。

■正規化(normalization)とは

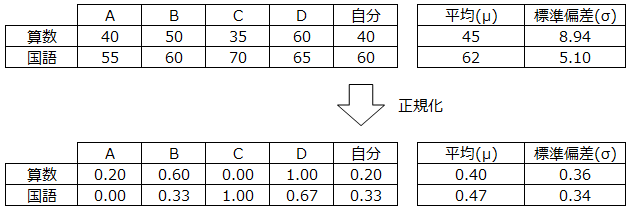
標準化と混同しやすい言葉に"正規化"があります。正規化はデータを一定のルールに基づいて整形する事で、例えば0～1の範囲に変換する場合、以下式で表すことがあります。 (正規化するやり方はいくつかあります)



先ほどの例について正規化すると以下となります。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 確率・統計 統計/解析 平均値、中央値、最頻値 平均値と期待値の違い 二乗平均、二乗和 移動平均 分散、標準偏差、共分散 偏差値 単回帰分析,最小二乗法 重回帰分析 リッジ回帰, ラッソ回帰 カーネル法, カーネル関数 ガウス過程回帰 エクセルによる回帰分析 最小二乗法の公式導出 主成分分析 疑似乱数, 準乱数 基底関数 仮説検定 モンテカルロ法 パレートの法則 データを正しく読む 有効サンプル数 ベイズ理論 ベイズの定理 ベイズの定理応用形 逐次ベイズ推定 ナイーブベイズフィルタとは 確率分布推定 確率分布推定(正規分布) MAP推定,最尤推定 ベイジアンネットワーク 確率 同時確率、条件付き確率 組み合わせの計算方法 確率変数 , 確率分布とは ・ベルヌーイ分布 ・二項分布 ・正規分布, ガウス分布 ・ポアソン分布 ・ベータ分布 ・ワイブル分布 ・カイ二乗分布 ・t分布 確率過程とは