確率分布のベイズ推定

■確率分布の推定
こちらで説明したのは、ベイズ推定によって事後の確率を推定するものでした。対してここでは母数を確率変数とした時の確率分布を推定する方法を説明します。母数とはこちらで説明した様に分布を特徴づける数のことをいい、正規分布では平均値や分散値、またはベルヌーイ分布では確率自体を母数として定義します。イメージは以下。

＜ケース①＞

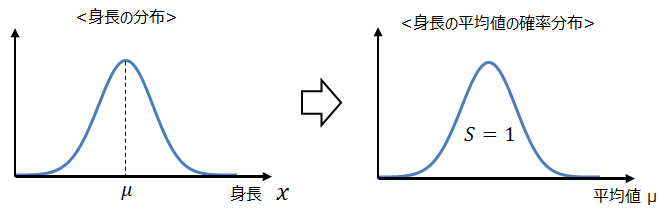
＜ケース②＞

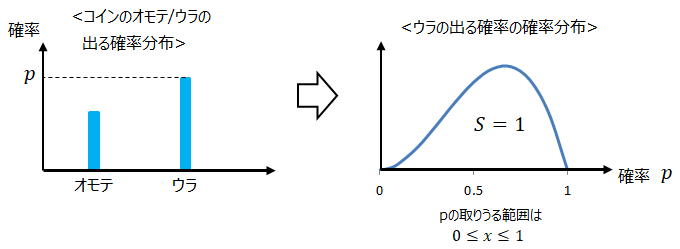
■ベイズの定理の変形
確率分布を推定するのにもベイズの定理の考えを使います。こちらでも説明した様にベイズの定理は以下。

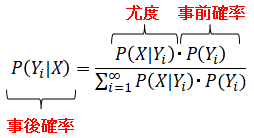
上記を以下の様に変形します。

これまで説明してきたのは、算出される値は事後確率という一つの値でしたが、事後分布という関数で表現されます。上記式のイメージを図で示すと以下になります。

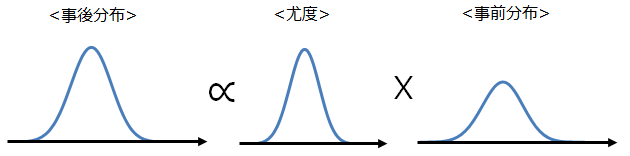
■例題
オモテの出る確率がθのコインがある。このコインを3回投げた時、オモテ、オモテ、ウラの順で出た。この時オモテの出る確率θの確率分布は？

1回目:オモテ

■事前分布
事前分布は現段階では情報は何もないので、一様分布と仮定します。この様な考えを理由不十分の原則といいます。

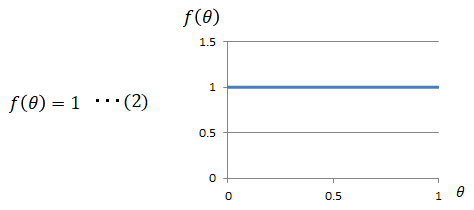
■尤度
オモテの出る確率がθの場合のオモテの出る確率となりますので、以下となります。

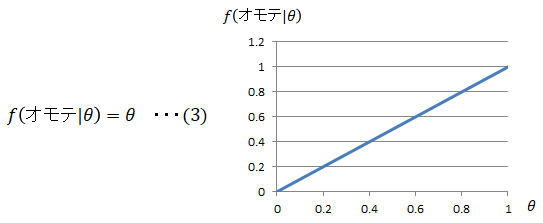
■事後分布
(2),(3)を(1)に代入すると、

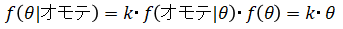
ここで確率の総和は1となるため、

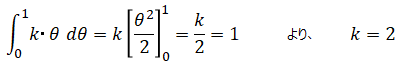
従って事後分布は以下となります。ここから解ることは、オモテが出る確率が1である確率が最も高くなり、またオモテが出る確率が0である確率は0となります(既にオモテが出たので当然となります)。

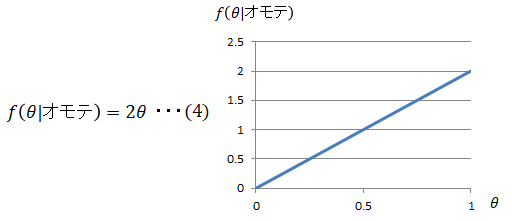
2回目:オモテ

■事前分布、尤度
(4)式が事前分布となり、(3)式が尤度となります。

■事後分布
(4)(3)式を(1)に代入すると、

ここで確率の総和は1となるため、

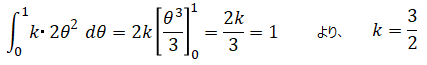
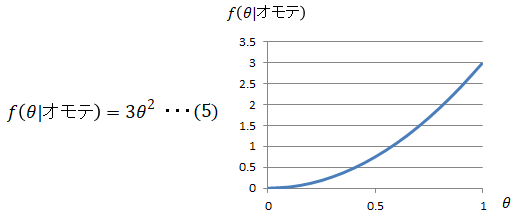
従って事後分布は以下となります。2回目もオモテが出たことで、オモテが出る確率が1になる確率が高くなりました。

3回目:ウラ

■事前分布
(5)式が事前分布となります。

■尤度
オモテの出る確率がθなので、ウラの出る確率は以下となります。

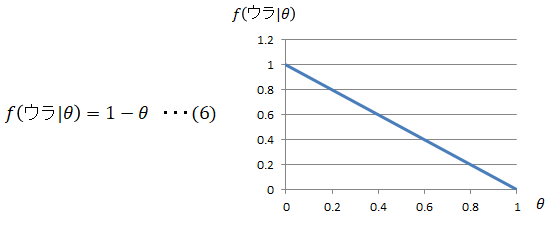
■事後分布
(5)(6)式を(1)に代入すると、

ここで確率の総和は1となるため、

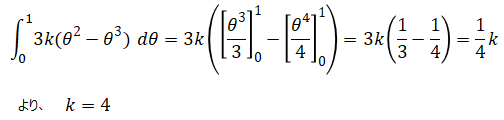
従って事後分布は以下となります。3回目にウラが出たことで、オモテが出る確率が1の確率はなくなりました。

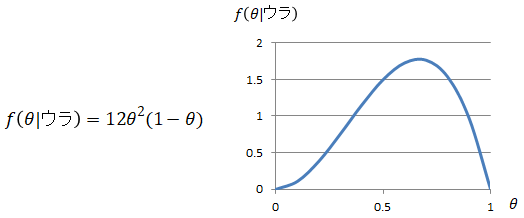
以上が確率分布の推定方法になります。