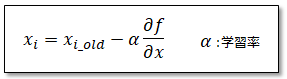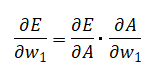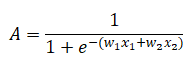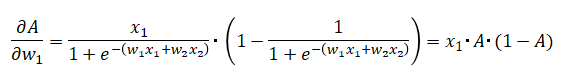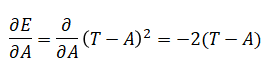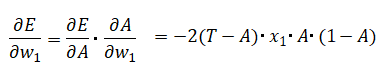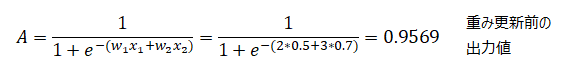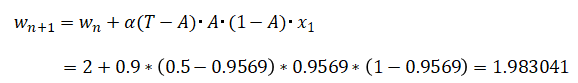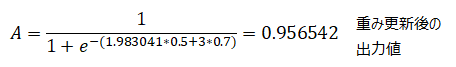勾配法の機械学習への適用

前提知識
　・勾配法(最急降下法)の原理
　・偏微分 , 連鎖率
　・ニューラルネットワークとは
　・シグモイド関数
　・誤差関数

こちらで勾配法の原理について説明しましたが、勾配法の機械学習への適用を考えます。勾配法とは関数の形が解らなかったり、微分することが難しい場合などにおいても、関数の最小値を遂次計算的に求める事ができる手法で、以下式で表されるものでした。



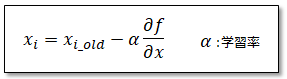
機械学習において勾配法で求める関数の最小値は真値とニューラルネットワークの出力値の誤差になり、その時の変数は重みwとなります。 誤差を求める関数を誤差関数(損失関数)といい、誤差関数値を最小にする時の重みwを勾配法にて求めていきます。上記式は以下で表すことができます。


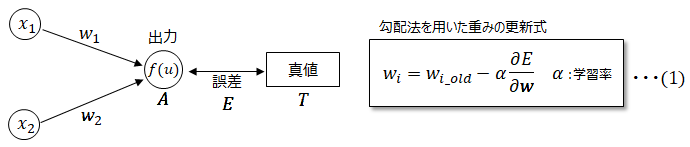
■誤差関数Eについて
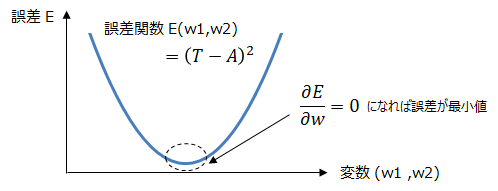
ここで扱う誤差関数は二乗和誤差とします。誤差関数値を最小にするためには微分値が0に近づけばよいです。



実際に誤差関数Eを各重みwについて微分します。例えばw₁について微分する場合、w₂は固定値として扱い、これを偏微分といいます。 またw₁はAの変数になっており、微分をやりやすくする為に連鎖律という考え方を用います。 この様にして全ての重みについて微分していきますが、ここではw₁を例にして説明します。


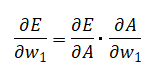
ここでAはニューラルネットワークからの出力値で以下となります。詳細はこちらを参照。


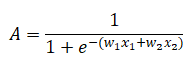
これをw₁について微分すると以下となります。シグモイド関数の微分の詳細はこちらを参照。


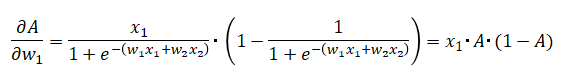
また、


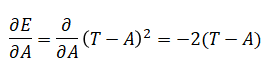
従って、


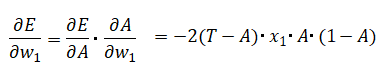
となります。これを(1)に代入しますが、上式の2は係数αに含めて考えてもよいので省略します。従って以下が誤差逆伝播法による重みw₁の学習式となります。 なおw₂の学習式は以下式のx₁がx₂となります。


■計算例
以下の入力および重みの時の出力値に対して真値は0.5であった。この時、より真値に近づく様に重みw₁を更新せよ。ただし学習率α=0.9とする



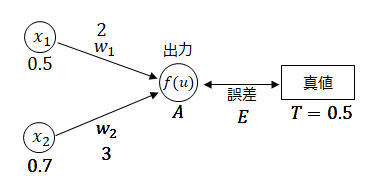
(2)より、


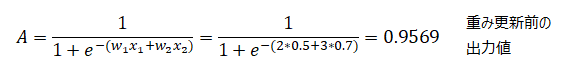
より、


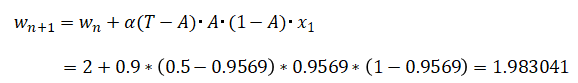
となりw₁が更新されました。実際に誤差が小さくなったのかどうか確認します。



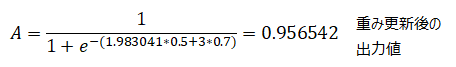
となり、僅かですが真値に近づくことが出来ました。実際にはこの動作を何回も繰り返すことで、より真値に近づくことになります。

誤差の収束値
今回の例において、誤差伝播法による重みの収束値(誤差がゼロになる値)は以下となります。誤差がゼロになる時の重みw₁とw₂の組み合わせのパターンは何種類もあります。 どこに収束するかは重みの初期値によって決まります。



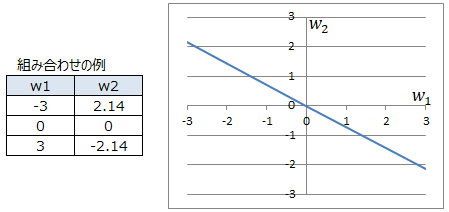
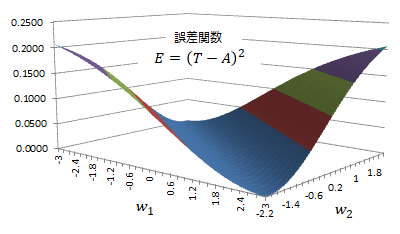
誤差関数Eと重みの関係を以下の様に示します。ここからも、誤差が最小値を取る領域が広くあることが分かります。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 機械学習 機械学習とは パラメトリックモデル 回帰,分類,クラスタリングの違い 分類(classification) 分類問題とは ナイーブベイズフィルタ 符号関数による分類 ロジスティック回帰 ・線形分離 ・非線形分離 サポートベクターマシン 決定木 k-近傍法 ニューラルネットワーク(NN) NNとは パーセプトロン 勾配法(最急降下法) ・機械学習への適用 損失関数(誤差関数) 誤差逆伝播法 交差検証 , ホールドアウト 活性化関数 ・ステップ , 符号関数 ・シグモイド ・ReLU ・Softmax ・tanh MNISTデータセット CIFAR-10データセット 画像認識方法 画像認識方法② 畳み込みNN(CNN) 再帰型NN(RNN) LSTM kerasによる実装例 ・NN ・CNN ・ディープラーニング クラスタリング k-means 強化学習 強化学習とは 価値関数 , ベルマン方程式 マルコフ決定過程 ε-greedy法 TD学習_スキナー箱 TD学習_Cartpole モンテカルロ法_Blackjack Deep Q-Network(DQN) ・DQNとは_スキナー箱 ・cartpole問題 ・Experience Replay 敵対的生成ネットワーク GAN DCGAN seqGAN seqGAN用文章データ作成