リッジ回帰, ラッソ回帰とは　pythonでの実装方法

リッジ回帰/ラッソ回帰とは、回帰分析の手法の一つで、損失関数に対して回帰式の係数の大きさに応じた損失の項を加える(正則化する)ことで過学習を抑えることができる手法です。これは、係数が大きいほど回帰式への入力に対する出力値の変動幅が大きくなり、過学習になりやすい傾向があるため、係数がなるべく小さい方が好ましいという考え方です。

リッジ回帰とラッソ回帰との違いは、正則化項の係数に対する損失の与え方が異なっており、リッジ回帰は「係数の二乗和」であるのに対して、ラッソ回帰は「係数の絶対値の和」であることです。これは、係数が基準からどれだけ離れているかを表現する考え方の違いで、リッジ回帰はユークリッド距離(そのためL2正則化項という)、ラッソ回帰はマンハッタン距離(L1正規化項)に基づいています。

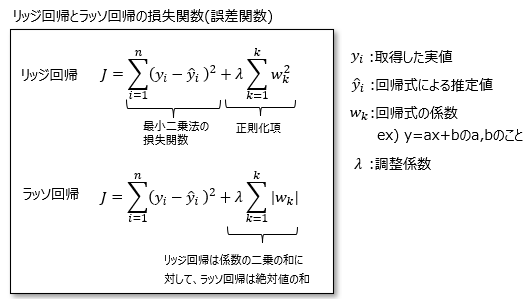
つまりこれらの回帰は言い方を変えると「ユークリッド距離あるいはマンハッタン距離で定義した所定領域の中で、誤差の二乗和が最も小さくなる様な係数をきめる(正則する)」と考える事ができます。

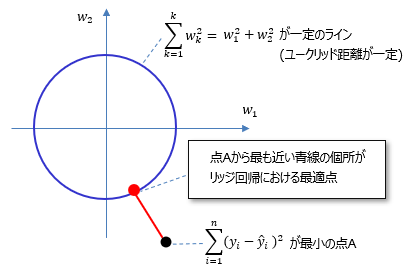
■パラメータ(係数)導出方法

リッジ回帰を例に説明します。上記リッジ回帰式をwで微分した結果が0になるところが、誤差の最小値となります。途中で転置行列を扱います。

■リッジ回帰の実装例 (python)

リッジ回帰のpythonによる実装例を説明します。実施した環境とライブラリは以下のとおり。

　・python ver：3.9
　・必要なライブラリ：numpy, matplotlib, scipy　インストール方法

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

x = np.array([-1, -0.8, -0.6, -0.4, -0.2, 0, 0.2, 0.4, 0.6, 0.8, 1])
y = np.array([ 2, 1.8, 1.7, 1.6, 1.8, 2, 2.2, 2.1, 2.0, 2.3, 2.4])

def ridge(w, x, y, d, lamda):
  y_ = np.poly1d(w)(x)
  error = np.sum((y - y_) ** 2) / len(y_) + lamda * np.sum(w ** 2)   # 損失関数(リッジ回帰)
  #error = np.sum((y - y_) ** 2) / len(y_) + lamda * np.sum(np.abs(w))   # 損失関数(ラッソ回帰)

  return error

d = 5     # 次数
lamda = 0.01    # 調整係数
w_init = np.ones(d+1)
result = minimize(ridge, w_init, args=(x, y, d, lamda), method="Nelder-Mead")   # 関数の値を最小化する
w = result.x   # 係数を出力

print(w)
plt.scatter(x, y)
plot_x = np.arange(-1,1.1,0.05)
plt.plot(plot_x, np.poly1d(w)(plot_x))   # グラフを描画
plt.show()

＜プログラム実行結果＞
結果は以下のとおり。プログラム内のdで回帰式の次数を設定し、lamdaで正則化項の調整係数を設定できます。 lamdaを0にすると、リッジ回帰ではない単なる最小二乗法にすることができます。

単なる最小二乗法の結果と比較すると、リッジ回帰はより高次の回帰式を設定しても過学習が無く設定できているのが解ります。

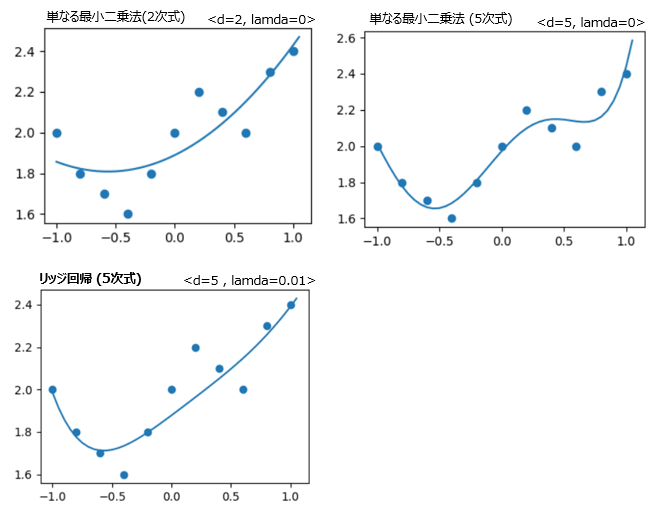
＜注意点＞
lamdaを大きくしすぎると、以下の様にうまくフィッティング出来なくなります。以下はlamda=0.1の場合です。

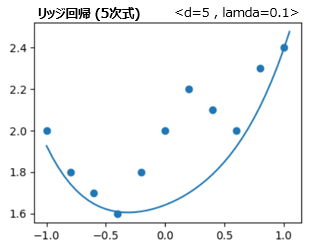
■ラッソ回帰の実装例 (python)

上記プログラムの損失関数の部分を、ラッソ回帰式に変えれば良いです(赤文字部分の一行を入れ替える)。

サブチャンネルあります。⇒ 何かのお役に立てればと

リッジ回帰, ラッソ回帰とは pythonでの実装方法