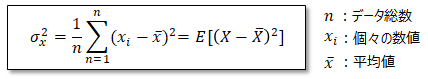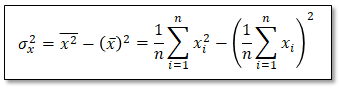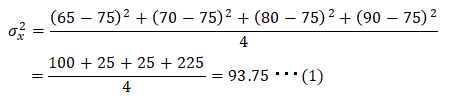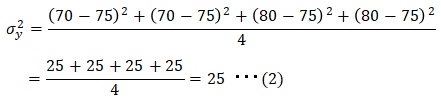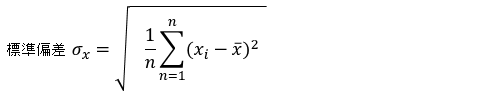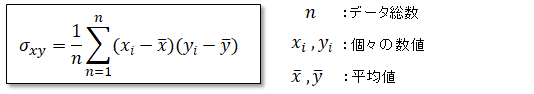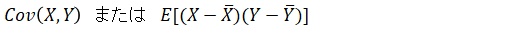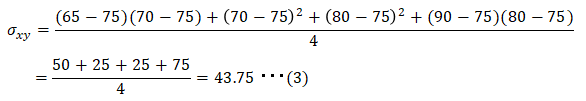分散　標準偏差　共分散の違いと定義　相関係数とは

・In English

■分散

分散σ²(シグマ二乗)とはデータの散らばり具合を示す指標で、以下で表します。 Eは期待値(平均)を意味します。



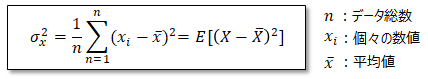
また上式は以下の様に変形可。



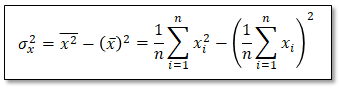
分散が何を意味しているのか具体例で考えます。4人の数学と国語のテストの点数が以下だったとします。どちらも平均点は同じ75点です。



分散とは平均値からの距離の二乗の総和を人数で割ったもの、つまり平均値からの距離の二乗、の平均なので、 この値が大きいという事は、平均値からのばらつきが大きい事を意味しております。 今回の例では、ぱっと見では数学と国語では国語の方が分散値が小さいように見えます。



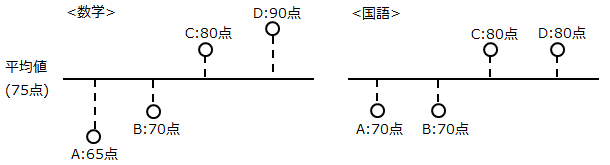
それでは実際に計算します。

■数学の点数の分散値


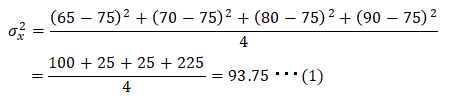
■国語の点数の分散値


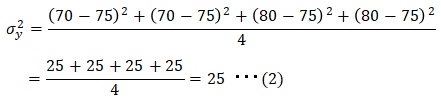
確かに国語の方が分散値が小さいことが解りました。

■標準偏差(SD:Standard Deviation)

なお分散の平方根を取ったのが標準偏差となり、以下式となります。



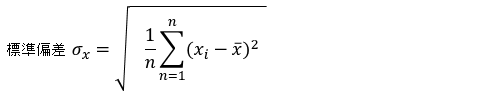
今回の場合、分散の単位は"点数²"であったのに対して、平方根を取ることで単位が"点数"になるため、 ばらつき度合いがイメージしやすいというのが標準偏差の特徴となります。またこれらデータから正規分布を描く方法はこちらになります。

■共分散(Covariance)

共分散とは2種類のデータの相関関係を示す指標で、以下式となります。



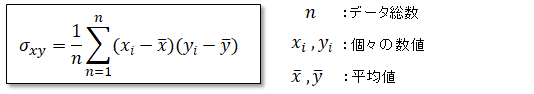
または以下の様にも表現します。



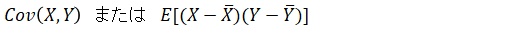
この値が、

　正ならば、一方の値が増加するともう一方の値も増加する、正の相関。
　負ならば、一方の値が増加するともう一方の値は減少する、負の相関。

となります。

これも具体例として上記で用いた数学と国語の点数の例で説明します。計算結果は以下のとおり。 結果として、国語の点数と数学の点数は正の相関があることが解りました。

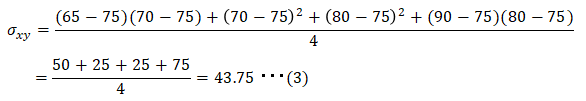
■相関係数

共分散を求めることで2種類のデータの相関関係を知ることが出来ましたが、値の大きさからは どれくらい相関関係が強いのかイメージしづらいです。そこで以下の様に値を正規化したのが相関係数となります。



相関係数は-1から1までの間を取り、以下の関係になっています。



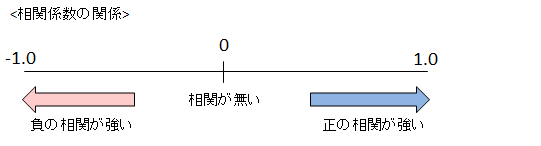
上記例で実際に計算します。(1)(2)(3)より、



となり、数学の点数と国語の点数は正の強い相関がある(数学の点数が高いと国語の点数も高い)ことが解りました。

■分散共分散行列

今回の例で説明してきた中で、数学の点数の分散σ_x²、国語の点数の分散σ_y²、数学と国語の相関関係を示す共分散σ_xyというものが出てきました。 これらを整理して解りやすくまとめたものを下記の様に表現し、これを分散共分散行列と言います。



なお、変数が3つの場合は以下の様になります。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 確率・統計 統計/解析 平均値、中央値、最頻値 平均値と期待値の違い 二乗平均、二乗和 移動平均 分散、標準偏差、共分散 偏差値 単回帰分析,最小二乗法 重回帰分析 リッジ回帰, ラッソ回帰 カーネル法, カーネル関数 ガウス過程回帰 エクセルによる回帰分析 最小二乗法の公式導出 主成分分析 疑似乱数, 準乱数 基底関数 仮説検定 モンテカルロ法 パレートの法則 データを正しく読む 有効サンプル数 ベイズ理論 ベイズの定理 ベイズの定理応用形 逐次ベイズ推定 ナイーブベイズフィルタとは 確率分布推定 確率分布推定(正規分布) MAP推定,最尤推定 ベイジアンネットワーク 確率 同時確率、条件付き確率 組み合わせの計算方法 確率変数 , 確率分布とは ・ベルヌーイ分布 ・二項分布 ・正規分布, ガウス分布 ・ポアソン分布 ・ベータ分布 ・ワイブル分布 ・カイ二乗分布 ・t分布 確率過程とは