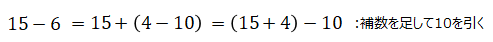トップメニュー加算器、減算器 |
|||||||
電気回路の基本・電気回路図の読み方の基本 ・オームの法則,キルヒホッフの法則 ・直列回路, 並列回路 ・電力 ・伝送損失 ・インピーダンス ・交流電流 ・回路素子外観 コイル・RL回路 ・電磁弁 , リレー コンデンサ・コンデンサの原理 ・RC回路 ・RC回路② ・RLC回路 ・RLC回路のインピーダンス ・Xコンデンサ, Yコンデンサ 半導体・半導体の原理 ・トランジスタ ・ダイオード ・還流ダイオード ・ツェナーダイオード ・整流回路 抵抗・プルアップ/プルダウン抵抗 ・終端抵抗 電圧変換器・変圧器(AC-AC) ・AC-DCコンバータ ・DC-DCコンバータ ・インバータ(DC-AC) オペアンプ・オペアンプの原理 ・反転増幅回路 ・コンパレータ デジタル回路・デジタル回路とは ・集積回路用語 ・論理回路 ・加算器、減算器 ・フリップフロップ ・シフトレジスタ ・マイコン構成要素 ・CPUパッケージの種類 ・メモリ(ROM等) ・フラッシュメモリ ・DRAM ・AD(アナログデジタル)変換 モーター・モータの種類 ・モータの構造, 部品名 ・モータの損失 ・モータの電流位相 ・ブラシ付きDCモータ ・ブラシレスDCモータ ・ACモータ(誘導電動機) ・3相/2相変換, クラーク変換 ・dq変換, パーク変換 ・正弦波生成, 三角波比較方式 ・ベクトル制御 センサ・温度センサ ・圧力センサ ・回転検出センサ ・加速度センサ ・ジャイロセンサ その他・ローサイド/ハイサイド駆動 ・回路の故障検出 ・ブレッドボード ・アース , 漏電ブレーカ ・T-T接地, T-N接地 ・感電の原因 ・サージ電流 ・Hブリッジ回路 ・PWM制御 ・スイッチの種類 ・クロック発生器 ・扇風機の分解 |
・In English
論理回路を使った加算器、減算器について説明します。2進数の考えが必要になります。 ■半加算器とは
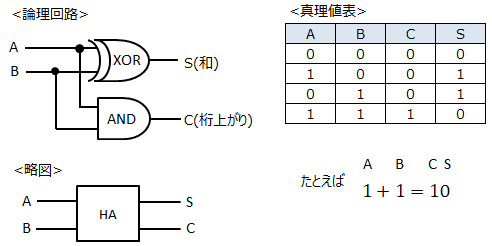
以下のとおり、XOR回路とAND回路の組み合わせとなります。1bit同士の加算となり、Sはsumの略で1桁目の加算結果、CはCarry(桁上がり)の略で2桁目の加算結果となります。
またこの加算器はHalf Adderと呼ばれ、HAと略して記載します。
■全加算器とは
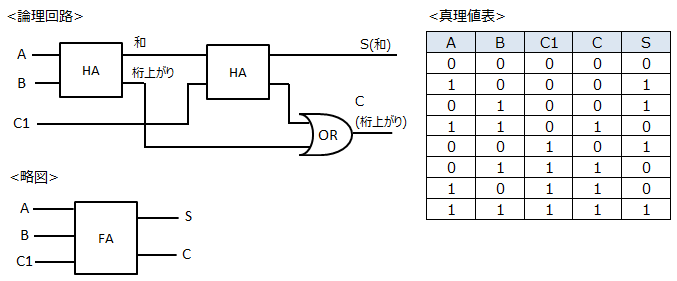
半加算器とOR回路の組み合わせとなり、一つ下の桁からの繰り上げを扱える形になります。この加算器はFull Adderと呼ばれ、FAと略して記載します。 ■4bit加算器とは
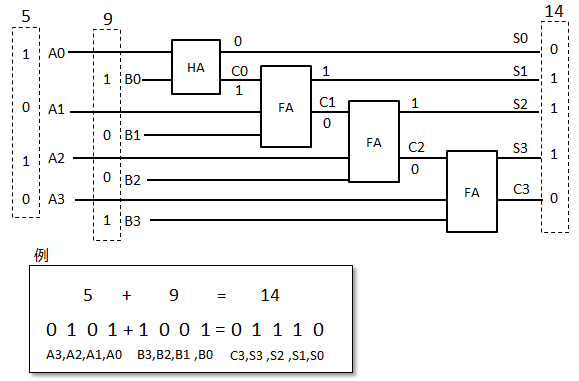
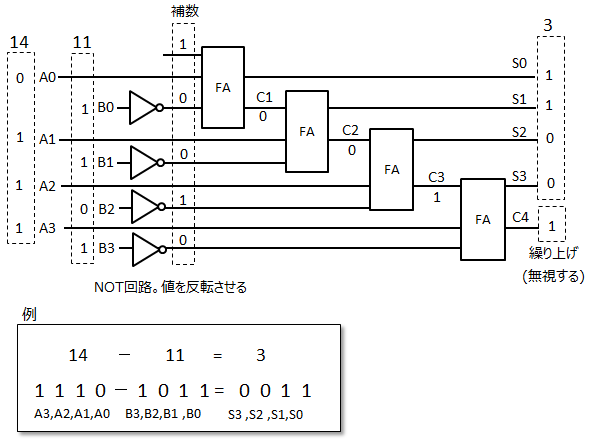
半加算器と全加算器を組み合わせると桁が多くなっても計算することが出来ます。具体例として5+9の結果を示します。 ■減算器とは
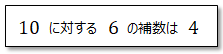
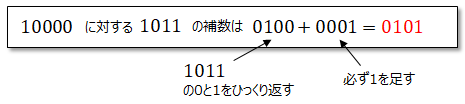
減算器は加算器で表現することが出来ます。その為には補数という考えが必要になります。
補数とは、足し算の答えが一定になる二つの数字があるとき、片方の数字に対するもう片方の数字が補数となります。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|
|||||
