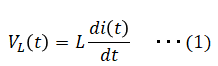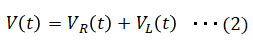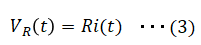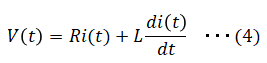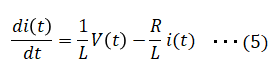電気回路(RL回路)

前提知識
　・電気回路の基本
　・Scilabとは

下記RL回路にて電圧V(t)を与えた時のコイル間電圧V_L(t)を考えます。


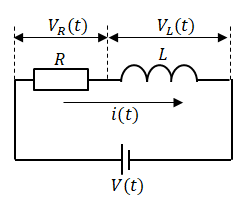
■コイルの性質
コイルの性質は電流変化を妨げる方向に起電力が発生します。従って電流が流れようとすると流れるのを妨げ、 電流が流れが止まろうとすると逆に電流を流すように働きます。電流変化が無い場合はコイル間の電圧は0になります。 V_L(t)はインダクタンス(L)と電流変化に比例し、以下となります。


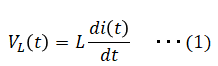
■RL回路の微分方程式の導出
キルヒホッフの法則より、回路全体の電圧の和は以下となります。


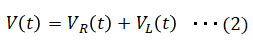
ここで抵抗間の電圧V_R(t)はオームの法則により以下。


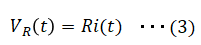
また(1)(3)を(2)に代入すると以下となります。


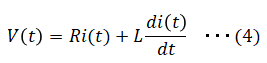
上記を以下の様に変形し、電流i(t)に関する微分方程式の形に表現することが出来ました。


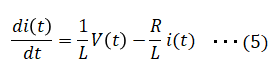
■Scilabで設計
(5)をブロック図で表現すると以下になります。


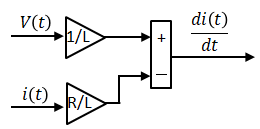
i(t)がまだ表現できていないですが、di(t)/dtを積分するとi(t)になるので、それを表現すると以下になります。


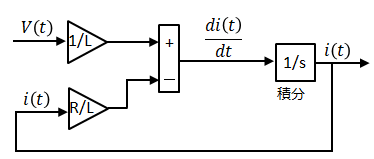
コイル、抵抗間の電圧を表現すると以下のとおり。


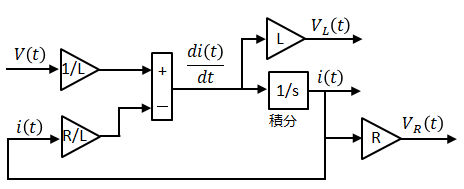
これをScilabで表現すると以下になります。



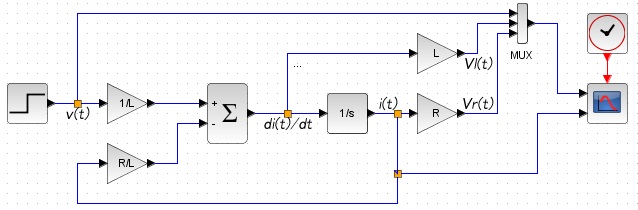
■動作確認結果
シミュレーション結果と各パラメータは以下のとおり。
　・V = 1(V)
　・R = 2(Ω)
　・L = 0.5(H)



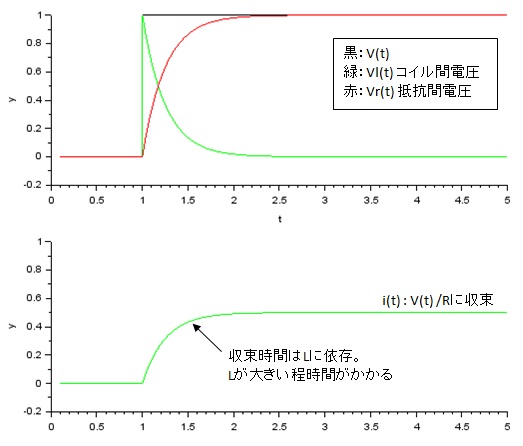
コイル間の電圧は、V(t)が変化した瞬間V(t)と同じ位の値となり、その後0に向かって収束します。これは高周波の電圧を 通過している事を意味し、このVl(t)の電圧を利用する回路をハイパスフィルタと言います。

一方抵抗間の電圧は、V(t)が変化した瞬間は値はすぐには反応せず、時間が経過するに従ってV(t)に収束します。 これは低周波の電圧を通過している事を意味し、Vr(t)の電圧を利用する回路をローパスフィルタと言います。


■補足
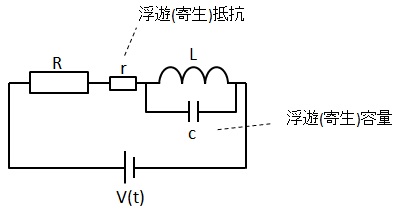
ローパス/ハイパスフィルタの類似回路としてRC回路がありますが、RL回路には以下の様に浮遊(寄生)抵抗、浮遊(寄生)容量があるため、 厳密に設計どうりのRL回路が作りづらいという難点があります。また一般的にコンデンサのほうがコストが安いです。よってRC回路を用いられることが多いようです。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 電気・電子回路 電気回路の基本 ・電気回路図の読み方の基本 ・オームの法則,キルヒホッフの法則 ・直列回路, 並列回路 ・電力 ・伝送損失 ・インピーダンス ・交流電流 ・回路素子外観 コイル ・RL回路 ・電磁弁 , リレー コンデンサ ・コンデンサの原理 ・RC回路 ・RC回路② ・RLC回路 ・RLC回路のインピーダンス ・Xコンデンサ, Yコンデンサ 半導体 ・半導体の原理 ・トランジスタ ・ダイオード 　・還流ダイオード 　・ツェナーダイオード 　・整流回路 抵抗 ・プルアップ/プルダウン抵抗 ・終端抵抗 電圧変換器 ・変圧器(AC-AC) ・AC-DCコンバータ ・DC-DCコンバータ ・インバータ(DC-AC) オペアンプ ・オペアンプの原理 ・反転増幅回路 ・コンパレータ デジタル回路 ・デジタル回路とは ・集積回路用語 ・論理回路 ・加算器、減算器 ・フリップフロップ ・シフトレジスタ ・マイコン構成要素 ・CPUパッケージの種類 ・メモリ(ROM等) ・フラッシュメモリ ・DRAM ・AD(アナログデジタル)変換 モーター ・モータの種類 ・モータの構造, 部品名 ・モータの損失 ・モータの電流位相 ・ブラシ付きDCモータ ・ブラシレスDCモータ ・ACモータ(誘導電動機) ・3相/2相変換, クラーク変換 ・dq変換, パーク変換 ・正弦波生成, 三角波比較方式 ・ベクトル制御 センサ ・温度センサ ・圧力センサ ・回転検出センサ ・加速度センサ ・ジャイロセンサ その他 ・ローサイド/ハイサイド駆動 ・回路の故障検出 ・ブレッドボード ・アース , 漏電ブレーカ ・T-T接地, T-N接地 ・感電の原因 ・サージ電流 ・Hブリッジ回路 ・PWM制御 ・スイッチの種類 ・クロック発生器 ・扇風機の分解