座標上の複数点の重心の求め方

・In English
前提知識
・平均値

座標に配置された複数点の重心の求め方を説明します。3点の重心の式は以下のとおり。各軸の平均値となります。



上記の場合、重心の計算結果は以下となります。



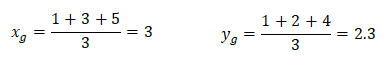
なお点が3つ以上ある場合においても、同様に平均値を求めれば良いです。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 数学 微分積分 ・微分公式 ・偏微分 ・数値微分 ・部分積分 ・ガウス関数の積分公式 複素数 ・複素数とは ・複素数を使う意味 フーリエ変換 ・フーリエ変換, FFTとは ・FFTの原理 ラプラス変換 ・ラプラス変換とは ・ラプラス変換の役割 線形代数 ・行列を使う目的, 定義 ・逆行列 , 行列式 ・行列の積 ・転置行列 ・行列の微分 ・固有値 ・ベクトルの内積 ・コサイン類似度 ・集合 ・写像 ・連立方程式を解く 指数　対数 ・対数関数 ・指数関数 , べき関数 ・デシベル その他 ・三角関数 ・階乗計算, ガンマ関数 ・arctan ,tanhの違い ・総和 Σ, 総乗 Π ・等差数列 ・有理関数のマクローリン展開 ・ニュートン法 ・重心 ・2乗に比例する関数 ・ラグランジュの未定乗数法 ・マンハッタン,ユークリッド ・帰納法, 演繹法 ・背理法 ・弧度法 ・スプライン曲線 ・| (バーティカルバー)