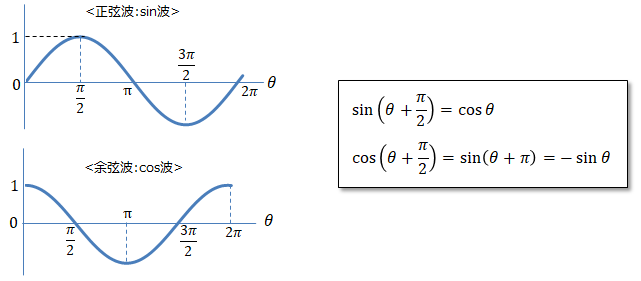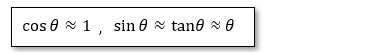トップメニュー三角関数 |
|||||||
微分積分・微分公式 ・偏微分 ・数値微分 ・部分積分 ・ガウス関数の積分公式 複素数・複素数とは ・複素数を使う意味 フーリエ変換・フーリエ変換, FFTとは ・FFTの原理 ラプラス変換・ラプラス変換とは ・ラプラス変換の役割 線形代数・行列を使う目的, 定義 ・逆行列 , 行列式 ・行列の積 ・転置行列 ・行列の微分 ・固有値 ・ベクトルの内積 ・コサイン類似度 ・集合 ・写像 ・連立方程式を解く 指数 対数・対数関数 ・指数関数 , べき関数 ・デシベル その他・三角関数 ・階乗計算, ガンマ関数 ・arctan ,tanhの違い ・総和 Σ, 総乗 Π ・等差数列 ・有理関数のマクローリン展開 ・ニュートン法 ・重心 ・2乗に比例する関数 ・ラグランジュの未定乗数法 ・マンハッタン,ユークリッド ・帰納法, 演繹法 ・背理法 ・弧度法 ・スプライン曲線 ・| (バーティカルバー) |
前提知識
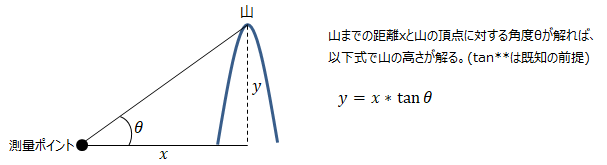
■三角比
三角比とは、直角三角形の辺の長さと角度の関係を表したもので、以下式で表します。 ■三角関数
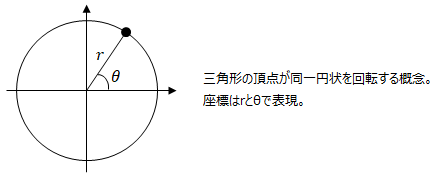
三角比は主に直角三角形の辺と角度の関係を表したものですが、三角関数は三角形の頂点が同一円状に回転するという概念で、その座標を円の中心から点までの直線距離と角度で表します。
この概念を用いる事で、単なる測量の用途だけには留まらず様々な事に利用できる様になりました。 ＜正弦波、余弦波＞
同一円状を回転する点を波の動きに見立てて表したのが正弦波と余弦波です。波の様な周期関数を三角関数で表現できることも利点の一つです。
sinとcosは位相が異なるだけの関係なので、波の形をみたらその関係を導けます。 ＜三角関数の微分＞
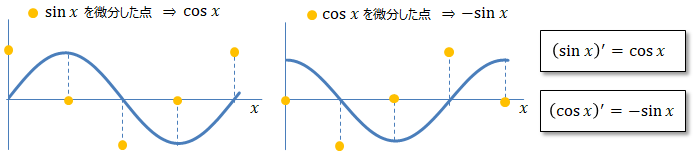
正弦波、余弦波をそれぞれ微分してプロットすれば、微分がどうなるか解ります。 ＜角度が十分小さいときの三角関数の近似＞
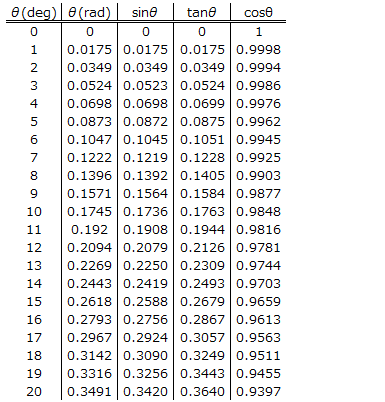
θが十分小さい時に以下が成り立ちます。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|
|||||
