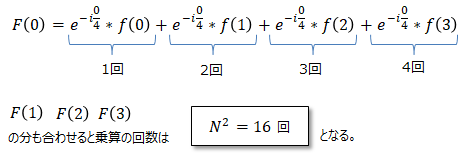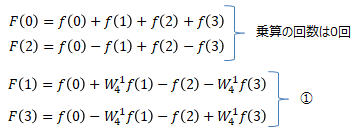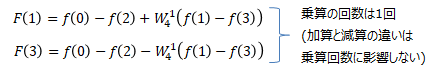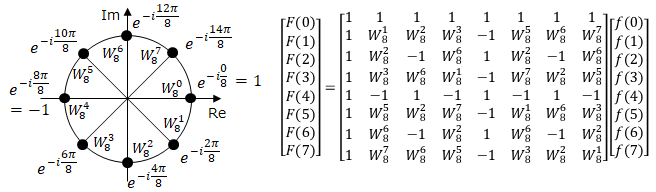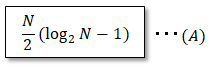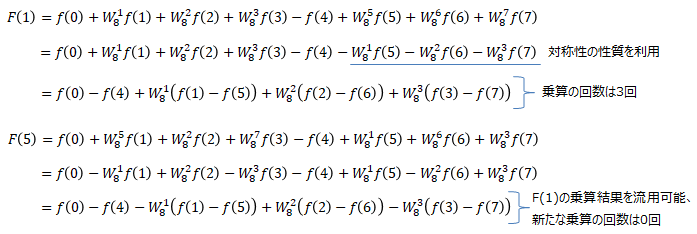高速フーリエ変換(FFT)の原理

　・In English
前提知識
　・高速フーリエ変換とは
　・複素数とは

■離散フーリエ変換(DFT)の計算量

高速フーリエ変換(Fast Fourier Transform:FFT)とは、離散フーリエ変換(Discrete Fourier Transform:DFT)の中でも演算を高速に行う手法の事ですが、どの様にして演算を高速にするのかその原理を説明します。 先ずFFTの演算式は以下でした。また具体例として、サンプリング数N=4の場合を行列で表します。

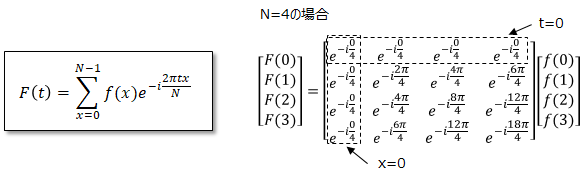
高速化されていない離散フーリエ変換の計算量は、コンピュータにとって計算負荷が高い乗算に注目すると、N^2となります。(上記例であるN=4の場合は16回)。 計算負荷の低い足し算や、複素指数部の乗算結果は既知として扱えるので、計算の回数からは除外します。

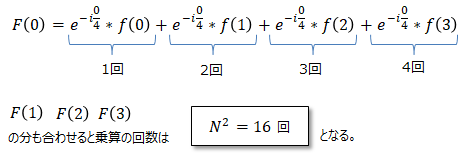
■高速フーリエ変換(FFT)の計算量

高速フーリエ変換の計算量簡略化の考え方は、簡単にいうと「同じ計算結果になるところはできるだけまとめ、重複して計算しない」です。N=4の時を具体例に考えます。

＜複素指数関数部分の簡素化＞
演算を簡素化する上で、複素指数関数部の重要な性質は周期性と対称性です。この性質を用いるために、Nは2の累乗(べき乗)である必要があります。

以下の様に複素平面上で表した時に、角度θが一周した時は値が同じになります。 更に円の中心を原点に対称位置にあるものは、マイナスを乗じたのと同じ値になります。すなわち複素指数部は4パターンに集約され、そのうち2パターンは値が1と-1なので乗算が不要になります。 更に、上下の点は対象はマイナスを掛けた値となるので、指数部のパターンは1パターンになります。



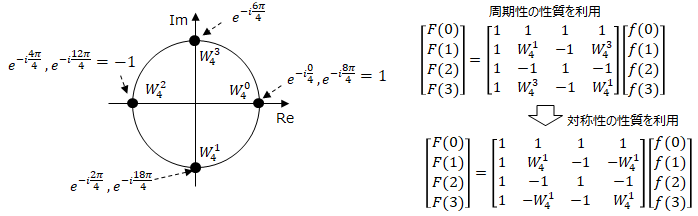
＜行列計算部分の簡素化＞
N=4の行列計算を書き出して、類似計算結果をまとめると以下となります。一つのペアは乗算を使っておりません。



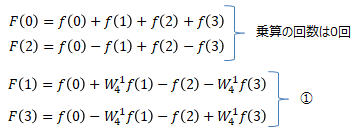
ここで①について、



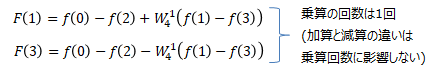
となり、トータルの乗算回数を1回に減らす事ができました。もともとは16回の乗算が必要だったことを考えると大幅な削減です。



＜N=8の時＞
N=4の時と同様、指数関数の周期性と対称性の性質を用います。



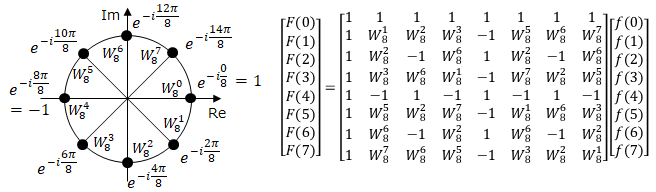
まず結論からいうとN=8の時の乗算の回数は8回で、これは一般解として以下式で表すことができます。なおN=4の時は成り立ちません。



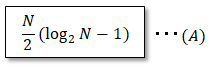
すなわち、DFTは64回に対してFFTで8回に減らすことができます。



それでは実際に行列計算を書き出してみます。ここで類似の計算結果同士を4つにまとめています。 式①で2回、式②③でそれぞれ3回なので、乗算は合計8回となります。



式①の計算


式②の計算


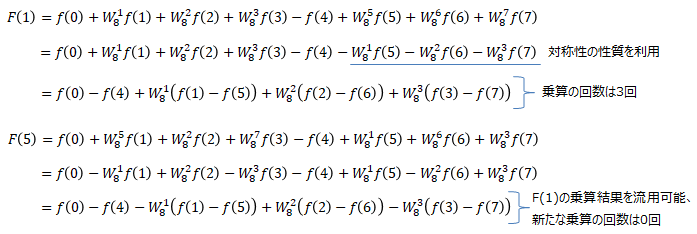
式③の計算
式②の計算と同様にすれば求める事ができます。

以上で高速フーリエ変換の計算原理の説明となります。N=16など、Nが大きくなっても(A)式で計算回数を求める事ができます。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 数学 微分積分 ・微分公式 ・偏微分 ・数値微分 ・部分積分 ・微分方程式 ・ガウス関数の積分公式 複素数 ・複素数とは ・複素数を使う意味 フーリエ変換 ・フーリエ変換, FFTとは ・FFTの原理 ラプラス変換 ・ラプラス変換とは ・ラプラス変換の役割 線形代数 ・行列を使う目的, 定義 ・逆行列 , 行列式 ・行列の積 ・転置行列 ・行列の微分 ・固有値 ・ベクトルの内積 ・ベクトルの外積 ・ベクトル場 ・コサイン類似度 ・集合 ・写像 ・連立方程式を解く 指数　対数 ・対数関数 ・指数関数 , べき関数 ・デシベル ・ネイピア数 その他 ・三角関数 ・素数 ・階乗計算, ガンマ関数 ・arctan ,tanhの違い ・総和 Σ, 総乗 Π ・∇, grad, div, rot ・等差数列 ・有理関数のマクローリン展開 ・ニュートン法 ・重心 ・2乗に比例する関数 ・ラグランジュの未定乗数法 ・マンハッタン,ユークリッド ・帰納法, 演繹法 ・背理法 ・弧度法 ・スプライン曲線 ・フィボナッチ数列 ・複利計算 ・| (バーティカルバー)