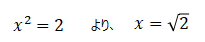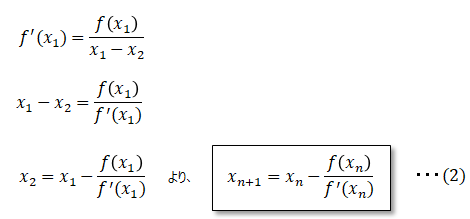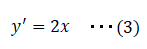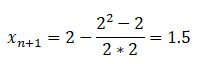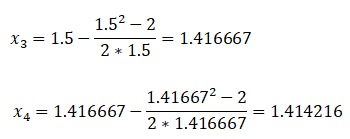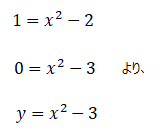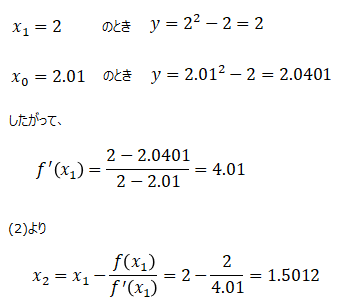ニュートン法

前提知識

■ニュートン法とは
例えば以下関数があったとします。


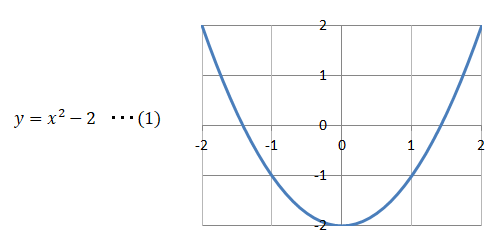
この式のy=0になる場合のxの値は以下となります。


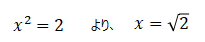
この√2という値は、解として求まったかのように思われますが、まだきちんとした数値にはなっていません。1.41421と知っている人は多いかと思いますが、これはただ単に暗記していたにすぎません。 数学的に考えると√1と√4の間、すなわち1と2の間にある事は解ります。このf=0の解(今回の場合は√2の解)を近似的に求める手法をニュートン法といいます。

■ニュートン法の考え方
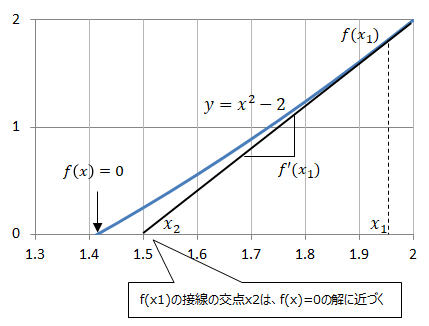
任意のx₁におけるf(x₁)の接線のx軸との交点x₂は、x₁よりf(x)=0の解に近くなる。

というものです。どういうことか、以下の図を見るとわかると思います。この様に、次はf(x₂)の接線のx軸の交点を求めて、 それを繰り返すことによりf(x)=0の解に近づけることが出来ます。


■ニュートン法を一般解で表現する
f(x₁)の接線の式はf(x₁)の微分となるので、


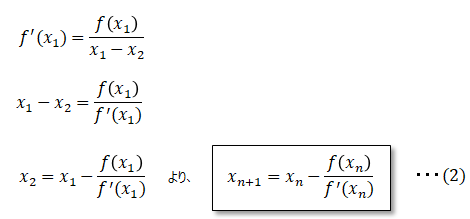
となります。

■具体例
上記式における解をニュートン法を用いて求めてみます。(1)式より、


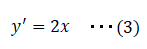
ここでx_nの値を適当に決めるとして、x_n=2とします。(1)(3)を(2)に代入して、


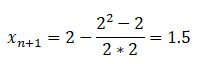
これを繰り返し計算すると、


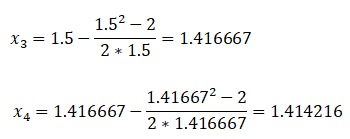
となり、繰り返し計算すればするほど真値に近づくのが解ります。

■ニュートン法の応用
＜応用①＞
f(x)=0のxの解だけではなく、f(x)=1の時のようなxの値も求めることが出来ます。式を以下の様にします。


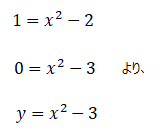
上記式においてf(x)=0の解を求めれば良いです。そこからは先ほど説明したニュートン法のとおりです。

＜応用②＞
以下の様な変曲点の値を求めたい場合は、微分した結果のf'(x)=0をニュートン法で解けば求まります。


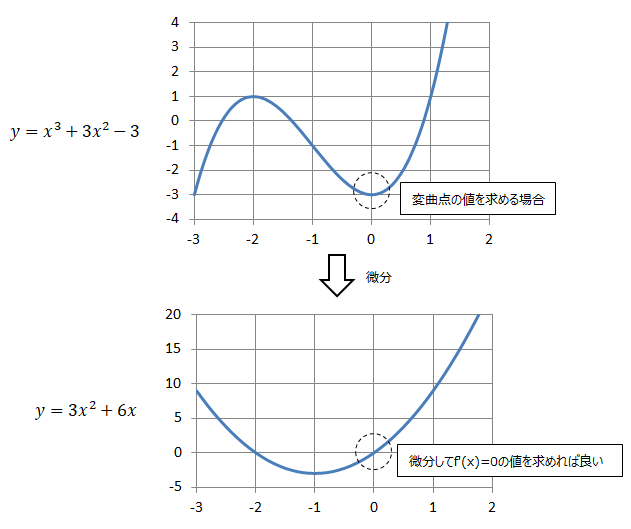
＜応用③＞
式の形が解らなくても、入力を与えた時の出力結果が解れば、微小な変化幅の2点の入力を与えた結果から接線の傾きを求めることが出来ます。


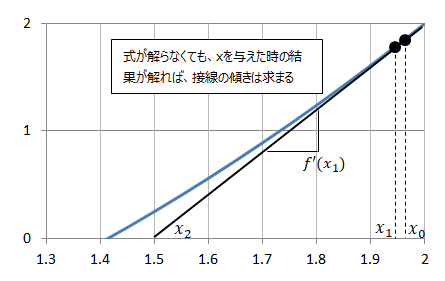
具体的に計算してみます。



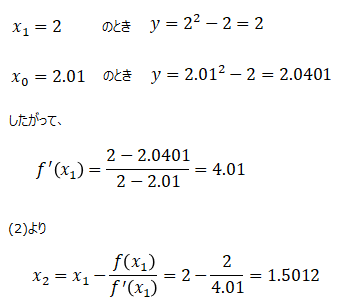
となり、先ほど求めた結果とほぼ等しくなることが分かります。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 数学 微分積分 ・微分公式 ・偏微分 ・数値微分 ・部分積分 ・微分方程式 ・ガウス関数の積分公式 複素数 ・複素数とは ・複素数を使う意味 フーリエ変換 ・フーリエ変換, FFTとは ・FFTの原理 ラプラス変換 ・ラプラス変換とは ・ラプラス変換の役割 線形代数 ・行列を使う目的, 定義 ・逆行列 , 行列式 ・行列の積 ・転置行列 ・行列の微分 ・固有値 ・ベクトルの内積 ・ベクトルの外積 ・ベクトル場 ・コサイン類似度 ・集合 ・写像 ・連立方程式を解く 指数　対数 ・対数関数 ・指数関数 , べき関数 ・デシベル ・ネイピア数 その他 ・三角関数 ・素数 ・階乗計算, ガンマ関数 ・arctan ,tanhの違い ・総和 Σ, 総乗 Π ・∇, grad, div, rot ・等差数列 ・有理関数のマクローリン展開 ・ニュートン法 ・重心 ・2乗に比例する関数 ・ラグランジュの未定乗数法 ・マンハッタン,ユークリッド ・帰納法, 演繹法 ・背理法 ・弧度法 ・スプライン曲線 ・フィボナッチ数列 ・複利計算 ・| (バーティカルバー)