複素数の必要性

前提知識
・複素数の基本

複素数の概念をこちらで説明しましたが、実用面で何のために使うのか、その必要性や利点を説明します。 複素数は実在する数ではないのですが、存在すると仮定して利用すると非常に都合が良くなります。

■バネの振動
バネは位置エネルギーと運動エネルギーの総和を一定に保ったまま、お互いのエネルギーを変換させながら動きます。 ただし、運動エネルギーは速度として観測することが出来ますが、位置エネルギーはバネ(重り)から直接測ることは出来なく、バネに内在したエネルギーと言えます。 この見えない位置エネルギーを虚数として扱い、運動エネルギーを実数として扱います。 エネルギーの損失が無い場合は単振動となり同心円状を動きますが、摩擦などのエネルギーの損失が有る場合は、徐々に減衰していくので円が小さくなっていきます。



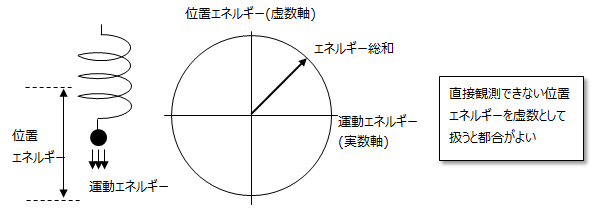
ここで、虚数成分を振動(周波数)成分を表し、実数成分を減衰として表すことができますが、 この様に複素数を振動と減衰に見立てた表現を複素周波数と呼びます。 この表現方法を利用すれば、以下の手法を用いて制御対象物の特性を解り易く表現する事ができます。

　・特性方程式を用いた安定性評価
　・ボード線図を用いたゲイン/位相特性の表現

■交流電力
交流電力の無効電力は実際には回路で消費されない仮想的な電力で、これを虚数で表現します。こうする事で交流電力を容易に求める事ができます。


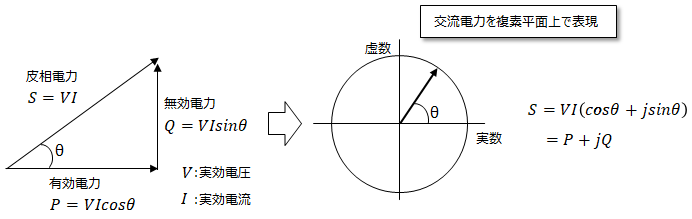
■周波数分析
周波数分析を行う際にもフーリエ変換で複素指数関数を用います。特にFFT(高速フーリエ変換)の際に計算を簡素化するためには複素指数関数の周期性、対称性の性質を用います。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 数学 微分積分 ・微分公式 ・偏微分 ・数値微分 ・部分積分 ・ガウス関数の積分公式 複素数 ・複素数とは ・複素数を使う意味 フーリエ変換 ・フーリエ変換, FFTとは ・FFTの原理 ラプラス変換 ・ラプラス変換とは ・ラプラス変換の役割 線形代数 ・行列を使う目的 ・行列の用語 , 定義 ・逆行列 , 行列式 ・行列の積 ・転置行列 ・行列の微分 ・固有値 ・ベクトルの内積 ・コサイン類似度 ・集合 ・写像 指数　対数 ・対数関数 ・指数関数 , べき関数 ・デシベル その他 ・三角関数 ・階乗計算, ガンマ関数 ・arctan ,tanhの違い ・総和 Σ, 総乗 Π ・等差数列 ・有理関数のマクローリン展開 ・ニュートン法 ・重心 ・2乗に比例する関数 ・ラグランジュの未定乗数法 ・マンハッタン,ユークリッド ・帰納法, 演繹法 ・背理法 ・| (バーティカルバー)