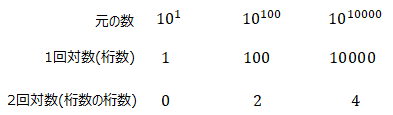対数とは　指数との関係

前提知識
　・べき乗関数、指数関数

指数と対数はべき乗の数を表現する手法ですが、以下の様にそれぞれ同じ意味のことを異なる表現で示しています。



■対数の公式


＜常用対数と自然対数＞
常用対数とは底10の場合の対数です。自然対数は底がネイピア数e(=2.718・・)の場合の対数です。lnと書けば自然対数ですが、logMという様に底を省略記載する場合、 常用対数か自然対数のどちらかを表します。これは分野によって習わしがあるので、その時の状況で判断します。

　

■対数の概念
対数は底を進数としたときの桁数を表しております(実際には対数に1を加える)。例えば以下。

　

対数を使用する具体例の一つとして、浮動小数点の有効桁数を調べるのに使います。

まれに対数を2回とる場合がありますが、それは桁数の桁数を表現しており、桁数がどれくらいの規模で変化しているかを把握する事ができます。

　

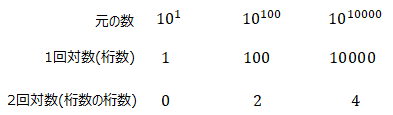
■対数のメリット
対数の概念は桁数ですが、物事を桁数で考える事で以下のようなメリットがあります。

① 大きい数を小さい数で表すことができ、規模間の把握が容易になる。
例えば単位にdB(デシベル)、pH(ペーハー)、マグニチュードなどがありますが、これは対数を使って変換されており、人間の感覚に合った単位になっております。

② 桁数の大きい数の掛け算や割り算を、計算の簡単な足し算や引き算に置き換える事ができる。
桁数は指数部を表している為、指数法則に基づいて指数部の足し算引き算が可能となります。こうする事で複雑な掛け算割り算を、割と簡単な足し算/引き算で済ます事ができます。

■対数グラフの見方
対数グラフとは、軸が対数スケールになっているグラフです。桁数をプロットする訳ではなく、値をプロットしていけば10目盛りで1桁変わる様な間隔が設定されています。桁数には0が無いため、対数軸には0をプロットする事ができません。



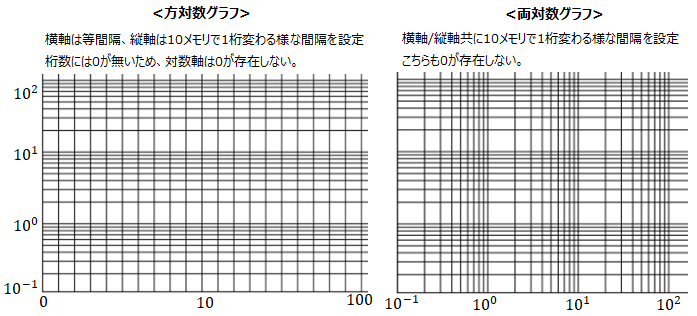
対数グラフを使うとべき関数や指数関数は線形で表せるので、逆にいうと、ある特性がべき関数/指数関数の特性に従っている否かを判断する事ができるのが利点の一つです。

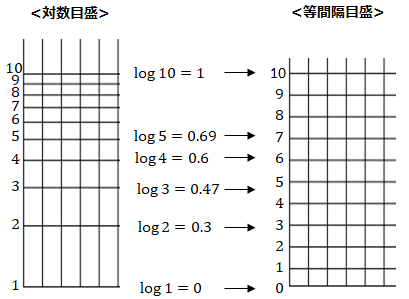
＜目盛りが等間隔ではない理由＞
対数の目盛りを等間隔の目盛りと対比させると、等間隔になっていないことが解ります。

サブチャンネルあります。⇒ 何かのお役に立てればと

関連記事一覧 トップメニュー 数学 微分積分 ・微分公式 ・偏微分 ・数値微分 ・部分積分 ・微分方程式 ・ガウス関数の積分公式 複素数 ・複素数とは ・複素数を使う意味 フーリエ変換 ・フーリエ変換, FFTとは ・FFTの原理 ラプラス変換 ・ラプラス変換とは ・ラプラス変換の役割 線形代数 ・行列を使う目的, 定義 ・逆行列 , 行列式 ・行列の積 ・転置行列 ・行列の微分 ・固有値 ・ベクトルの内積 ・ベクトルの外積 ・ベクトル場 ・コサイン類似度 ・集合 ・写像 ・連立方程式を解く 指数　対数 ・対数関数 ・指数関数 , べき関数 ・デシベル ・ネイピア数 その他 ・三角関数 ・素数 ・階乗計算, ガンマ関数 ・arctan ,tanhの違い ・総和 Σ, 総乗 Π ・∇, grad, div, rot ・等差数列 ・有理関数のマクローリン展開 ・ニュートン法 ・重心 ・2乗に比例する関数 ・ラグランジュの未定乗数法 ・マンハッタン,ユークリッド ・帰納法, 演繹法 ・背理法 ・弧度法 ・スプライン曲線 ・フィボナッチ数列 ・複利計算 ・| (バーティカルバー)