帰納法と演繹法と仮説推論(アブダクション)の違いを具体例で説明 |
|||||||
・微分公式 ・偏微分 ・数値微分 ・部分積分 ・微分方程式 ・ガウス関数の積分公式 ・複素数とは ・複素数を使う意味 ・フーリエ変換, FFTとは ・FFTの原理 ・ラプラス変換とは ・ラプラス変換の役割 ・行列を使う目的, 定義 ・逆行列 , 行列式 ・行列の積 ・転置行列 ・行列の微分 ・固有値 ・ベクトルの内積 ・ベクトルの外積 ・ベクトル場 ・コサイン類似度 ・集合 ・写像 ・連立方程式を解く ・対数関数 ・指数関数 , べき関数 ・デシベル ・ネイピア数 ・三角関数 ・素数 ・階乗計算, ガンマ関数 ・arctan ,tanhの違い ・総和 Σ, 総乗 Π ・∇, grad, div, rot ・等差数列 ・有理関数のマクローリン展開 ・ニュートン法 ・重心 ・2乗に比例する関数 ・ラグランジュの未定乗数法 ・マンハッタン,ユークリッド ・帰納法, 演繹法 ・背理法 ・弧度法 ・スプライン曲線 ・フィボナッチ数列 ・複利計算 ・| (バーティカルバー) |
■帰納法と演繹法と仮説推論(アブダクション)の違い
帰納法とは、複数の個別事象から共通項を見つけ、一般的な原理原則を導く手法です。例えば以下のとおり。
① 先週の金曜日の夕食はカレーだった (個別事象)
演繹法とは、一般的な原理原則から個別事象を推論する手法です。演繹法の典型例に三段論法があります。以下例のとおり。
① 毎週金曜日の夕食はカレーが出る (原理原則)
① 毎週金曜日の夕食はカレーである事が分かっている (原理原則)
<帰納法と演繹法と仮説推論の違いまとめ>
■数学的帰納法数学的帰納法とは、帰納法を数学における事象に当てはめたもので、代表的なパターンとして以下があります。
① 自然数n=1の時に、ある事象Xが成り立つ
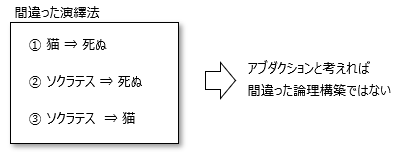
■演繹法が成り立たない例
以下は間違った演繹法の有名な例ですが、これはアブダクションによる仮説推定と考えたら間違った論理構築ではありません。
(仮説が正しいかどうかは別ですが)
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|
|||||