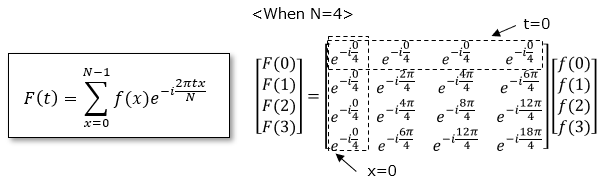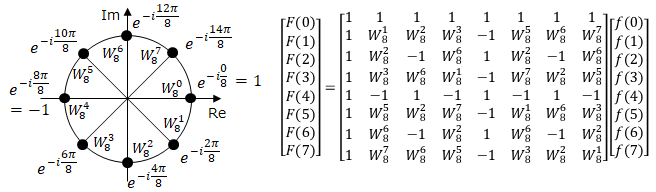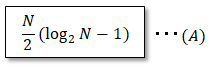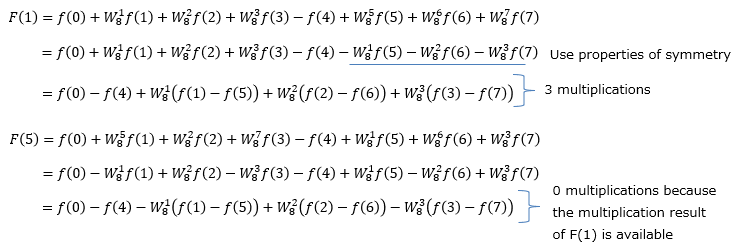Fast Fourier Transform (FFT) is a method of performing calculations at high speed among Discrete Fourier Transform (DFT).
I will explain the principle of how to speed up the calculation. The calculation formula for FFT is as follows.
As a concrete example, the case of sampling number N = 4 is represented by a matrix.
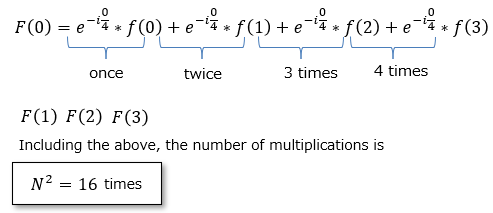
The computational complexity of DFT is N2, focusing on multiplication, which is computationally intensive for the computer (16 times for N=4).
Additions with low computational load and multiplication results of complex exponents can be treated as known, so they are excluded from the number of computations.
■Complexity of Fast Fourier Transform (FFT)
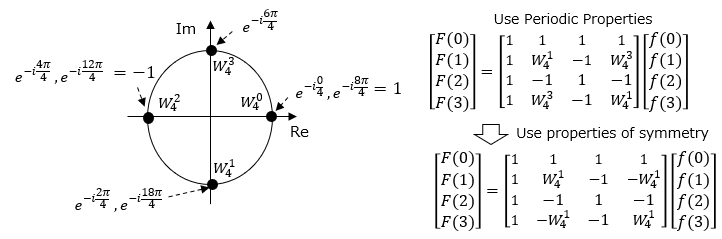
The idea of reducing the amount of calculation of FFT is "Do not calculate where the same calculation result is obtained".
Consider the case of N=4 as a concrete example.
＜Simplification of complex exponential＞
Important properties of the complex exponential part for simplifying arithmetic are periodicity and symmetry.
To use this property, N must be a power of two.
When expressed on the complex plane as shown below, the values are the same when the angle θ goes around.
Furthermore, if the center of the circle is symmetrical with the origin, it will be the same value as multiplied by -1. In other words, the complex exponent part is aggregated into 4 patterns, 2 of which have values of 1 and -1, so no multiplication is required.
Furthermore, since the upper and lower points are multiplied by a negative value, the pattern of the exponent part becomes 1 pattern.
＜Simplification of the matrix calculation＞
If you write out the matrix calculation of N = 4 and summarize the similar calculation results, it will be as follows.
As a result, we were able to reduce the total number of multiplications to one. A significant reduction considering that it was originally 16 multiplications.
＜When N=8＞
As with N=4, we use the periodicity and symmetry properties of the exponential function.
From the conclusion, the number of multiplications when N = 8 is 8 times, which can be expressed by the following formula as a general solution. It does not hold when N=4.
Even if N becomes large, such as N=16, the number of calculations can be calculated using the following formula.
That is, the DFT is 64 times, while the FFT can be reduced to 8 times.
Now let's actually write out the matrix calculation. Here, similar calculation results are grouped into four groups. There are 2 multiplications in formula (1) and 3 times in formulas (2) and (3), so the total number of multiplications is 8.
Calculation of formula ①
Calculation of formula ②
Calculation of formula ③
It can be obtained in the same way as the calculation of formula (2).
TOP MENU
