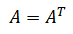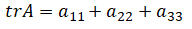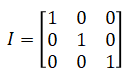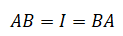What is a matrix? Purpose and types of matrices

・In Japanese

■What is a matrix?

A matrix is ​​an arrangement of numbers or variables. For example, the following is a matrix with 2 rows and 2 columns. Each number in a matrix is ​​called an element or component.

■Purpose and examples of using matrices

The purpose of using matrices is to make even complex calculations easier to understand by integrating numerical values ​​and formulas into one matrix. The following are examples of how matrices are used.

■Types of matrices

＜Square matrix＞
A matrix in which the number of rows and columns is the same is called a square matrix, and a square matrix of size n x n is called an nth order square matrix.



＜Symmetric matrix＞
A matrix that is symmetric (has the same values) across the main diagonal of a square matrix is ​​called a symmetric matrix.



The transpose of a symmetric matrix is ​​equal in value.



＜Diagonal matrix＞
The elements on the main diagonal of a symmetric matrix are called the diagonal elements, and a matrix whose values ​​other than the diagonal elements are all zero is called a diagonal matrix.



Diagonal sum, Trace
The sum of the diagonal elements of the diagonal matrix above is called a trace, which is defined as follows:



＜Identity matrix＞
A diagonal matrix whose diagonal elements all have the value 1 is called an identity matrix.



＜Regular matrix＞
When an inverse matrix exists for an n-th order square matrix A, A is called a regular matrix, and the following holds:

List of related articles TOP MENU Mathematics ・Exponential function ・Arctan, tanh ・Matrix multiplication ・Transposed matrix ・Fourier transform ・Fast Fourier Transform ・Matrix derivative ・Manhattan/Euclidean distance ・Centroid ・Vertical bar ・Gaussian integral ・Cosine similarity ・summation Σ, product Π ・Decibel[dB] ・Numerical Differention ・Induction,deduction,abduction ・Spline curve ・Lagrange's Method of Undetermined Multipliers ・Purpose of the matrix ・Proof by contradiction ・Vector field