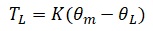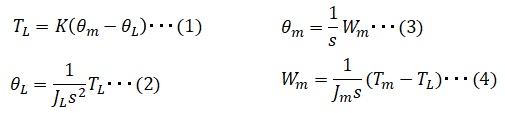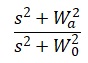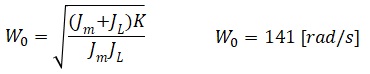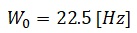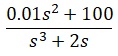モーターと低剛性負荷の回転運動体の微分方程式

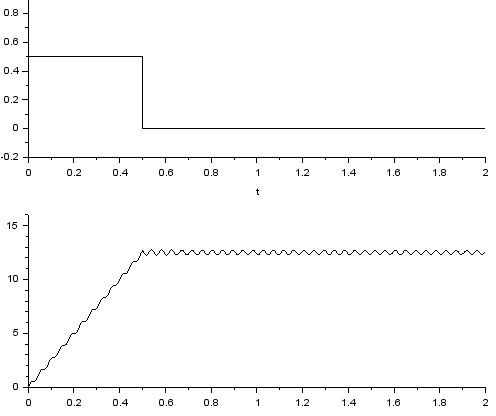
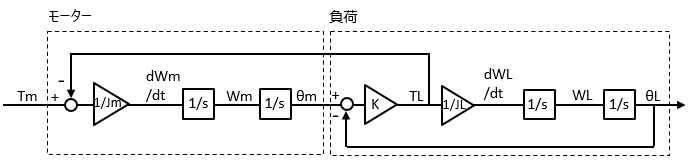
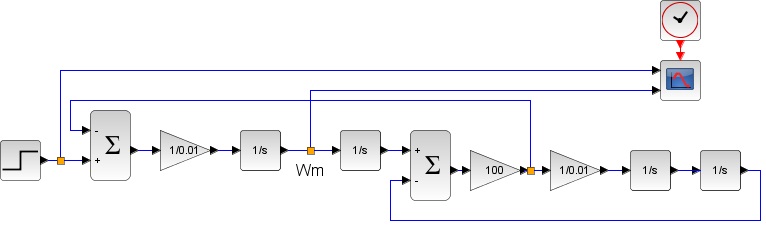
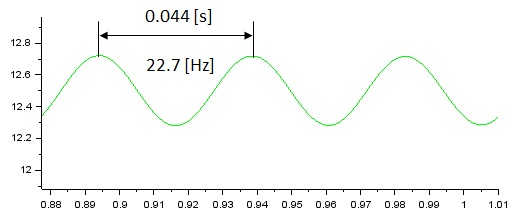
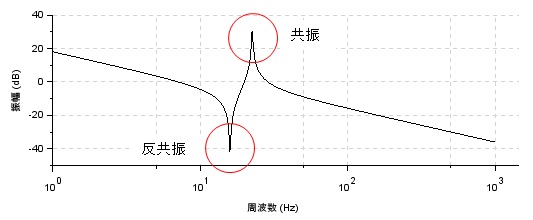
こちらでモーターと回転運動体の微分方程式について説明しました。次に、回転運動体が低剛性負荷の場合の微分方程式について説明します。低剛性の負荷の場合、モーターが発生したトルクに対して負荷を繋ぐシャフトがねじれながらトルクが伝わるという事になります。以下のとおり各パラメータを定義します。

＜ねじり剛性とは＞
シャフトがねじれた時に負荷に伝わるねじりトルクTLは、モーターと負荷の差回転が大きい程伝わるトルクが大きくなるため、以下となります。単位ねじり量当たりに必要なトルクをねじり剛性といいます。

■ブロック図/Scilab設計結果
上記システムをブロック図で表現すると以下となります。

Scilabで記述すると以下になります。

■シミュレーション結果
パラメータは以下のとおり。結果として角速度が変動しているのが解ります。

　・Jm=0.01 , JL=0.01 , K=100

■振動の周波数を調べる
振動の周波数(共振周波数)を調べるため伝達関数を求めます。以下のとおり。

上記伝達関数の共振周波数は下記式のW₀となります。

従って、

ここでw=2πfより、以下となります

それではシミュレーションでの周波数と比較してみます。先のシミュレーション結果を拡大して計測すると、一山の時間が約0.044秒なので周波数にすると22.7Hzとなり、計算結果とほぼ一致します。

またボード線図で表現すると以下となり、22.5Hzあたりで共振していることが解ります。なお、それより小さい周波数でゲインが小さくなっている箇所があると思います。これを反共振と言います。Scilabでのボード線図の描き方はこちらを参照。

それでは次に、この振動を除去する方法としてノッチフィルターを説明します。こちらをクリック。

サブチャンネルあります。⇒ 何かのお役に立てればと