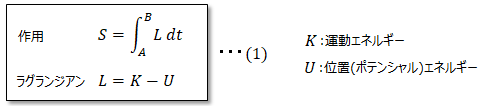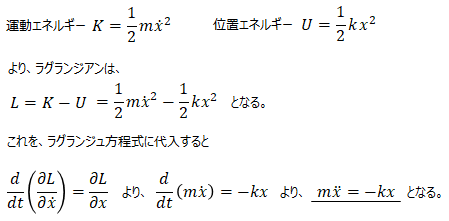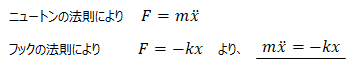|
前提知識
・ニュートンの法則
・運動エネルギー、位置エネルギー
■最小作用の原理
最小作用の原理とは「物質がある地点からある地点まで移動する際、作用(時間やエネルギー等)が最小になる様な経路を選択する」という原理です。
例えば以下の様な光の屈折において、光がある地点まで到達するのに時間を最小にする様な経路が選択されています。

質量を持った物質が他地点(A⇒B地点)に移動する場合、最小作用の原理を表現できる作用は以下の様に運動エネルギーと位置エネルギーで表すことができ、これをラグランジアン Lといいます。これは理論的にで求めた訳ではなく「この様に定義したらうまく説明する事ができた」、経験則で求めた式です。
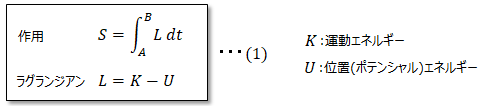
■ラグランジュの運動方程式
ラグランジュの運動方程式とは最小作用の原理を満たす事を前提に解いた運動方程式で、古典力学が主に力の作用の関係を運動方程式として表しているのに対して、ラグランジュの運動方程式はエネルギーで表現しているのが特徴です。
式はラグラジアンを最小にする為に(1)式を微分した結果が0になる値を求める形となっております。導出過程は省略しますが結果は以下のとおり。

この方程式の嬉しさは、古典的な手法より簡単に運動方程式を立てる事ができる場合がある所にあります。
<具体例>
まずは、古典力学によって運動方程式を立てた場合とラグランジュの運動方程式を使った場合で等価であることを確認します。以下のバネ運動を考えます。
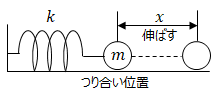
■ラグランジュ方程式の場合
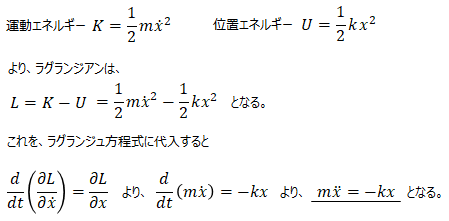
■古典力学の場合
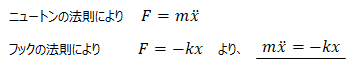
となり、両者が等価であることが確認できた。
<具体例②>
より複雑な事例として倒立振子の運動方程式を求めます。こちらを参照。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|