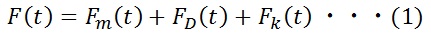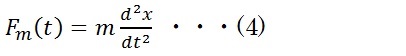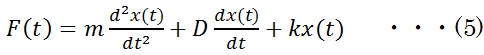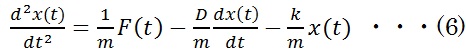バネマスダンパ系

バネマスダンパ系の運動方程式/微分方程式の導出方法の説明、およびバネマスダンパのモデルの構築、シミュレーションによる動作確認を行います。下記図の様なバネマスダンパ系に、力F(t)を与えた時の変位量x(t)を求めます。

F(t)はバネ、マス、ダンパそれぞれからの反力の合計となりますので、以下式となります。

それぞれにかかる力は以下のとおり。

＜バネの運動方程式＞

フックの法則により、バネにかかる力はバネ定数kとバネの変位量x(t)に比例するため、以下となります。

＜ダンパの運動方程式＞

ダンパという物は、例えば車のサスペンションについている様な部品で、ショックアブソーバー(振動減衰装置)とも呼ばれます。イメージとしては円筒状の部品(シリンダ)の中に油が入っているピストンの様なもので、ピストンを思い切り押してもすぐには進まず、これがショック吸収の役割を果たしています。イメージ図は下記のとおり。

ダンパにかかる力は位置とは関係なく、ダンパが動く速度に比例します。これはピストンをイメージしたら解ると思いますが、ゆっくりピストンを押したら押す力は小さく、早くピストンを押したら押す力は大きくなり、これはピストンがどの位置にあっても変わらないと思います。従ってダンパにかかる力FD(t)は、粘性減衰係数Dとダンパの速度v(t)から以下のとおり表せます。

また、速度v(t)は位置x(t)の微分であるため上記式を以下のとおり変形します。

＜マスの運動方程式＞

マスは単なる質量のある物体で、質量mの物体にかかる力Fmと加速度aの関係はニュートンの運動方程式により以下となります。

また、加速度は速度の微分、速度は位置の微分で表すことが出来ますので、加速度は位置を2回微分した形で表すことが出来ます。

＜バネマスダンパ系の微分方程式の最終系＞

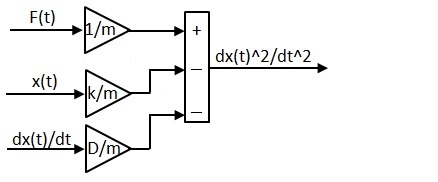
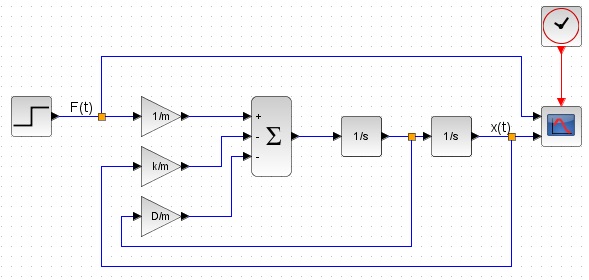
(2)(3)(4)式を(1)に代入します。

■バネマスダンパ系のモデルをScilabで設計

(5)式をScilabで設計するのですが少しコツがいります。力を与えた時の変位量x(t)を最終的に求めたいのですが、先ずは以下の様に変形します。

これをブロック図で表現すると以下になります。

こうしてみると、dx(t)/dtや、x(t)が表現できていませんが、dx(t)^2/dt^2を積分すれば求まることが解ります。それをブロック図で表現すると以下になります。

Scilabで表現すると以下になります。

■バネマスダンパ系の動作のシミュレーション結果

シミュレーション結果と各パラメータは以下となります。
　・k　= 0.5 [N/m] : ばね定数
　・m　= 2 [kg] : 質量
　・D　= 1 [N/(m/s)] : 粘性減衰係数

サブチャンネルあります。⇒ 何かのお役に立てればと