|
前提知識
・Scilabとは
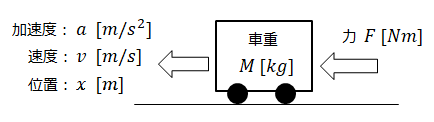
以下トロッコに力Fを加えた時のトロッコの加速度、速度ついての微分方程式を求めます。加速度はニュートンの法則(ma=F)を用います。先ずは路面との摩擦は無視できるほど小さいものとします。
微分方程式の導出は以下。

以上で微分方程式が求まりました (非常に簡単です)。
■Scilabで動作を確認する
Scilabで動作を確認します。上記微分方程式をブロック図で表すと以下になります。

こうしてみると、微分方程式と言っていた割に微分が無く、その代わりに積分があるのが解ります。上記にて"速度は位置の微分"という様に、微分という言葉を使って表現をしており、
それはおそらく多くの人が使う表現かと思いますが、それは我々は加速度より速度、速度より位置を容易に観測できる為、観測できる状態量から観測が難しい状態量を表現することになるので、
結果微分という表現を多く用いているのではないかと私は思ってます。しかし実際の物理現象としては、まず力から加速度が発生し、加速度の積分で速度が発生し、速度の積分から位置が決まるという様に、微分ではなく積分で成り立っています。
Scilabの設計結果は以下となります。車重は適当に2kgとします。

シミュレーション結果は以下のとおり。摩擦の影響が無いため、一度力を加えた後は力を加えなくてもトロッコは進んでいくのが解ります。

<摩擦の影響を考慮する>
タイヤの摩擦はこちらでも説明しておりますが、転がり抵抗として以下で表すことが出来ます。

転がり抵抗を考慮すると(1)式は以下となります。

Scilabでの設計結果は以下のとおり、転がり抵抗は速度が出ている時のみ影響するので、それを考慮しております。

シミュレーション結果は以下のとおり。摩擦の影響で次第に速度が低下し、いずれは停止するのが解ります。

サブチャンネルあります。⇒ 何かのお役に立てればと
|
|








