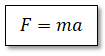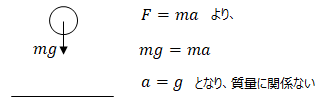|
■ニュートンの法則
ニュートンの法則とは、力と運動の関係を表す3つの法則の事です。
第1法則:慣性の法則
物体は力を受けるまでその状態を維持し続ける(静止している物は静止し続け、動いている物は等速で動き続ける)
第2法則:運動の法則
物体の加速度aは物体に与える力Fに比例し、物体の質量mに反比例する。以下式で表す事ができる。
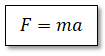
第3法則:作用反作用の法則
物体に力を与える時、与えた力と同じ大きさの反対向きの力を、与えた側も受ける。
<物体の質量によらず落ちる速さは同じ>
ガリレオガリレイが「落ちる速度は物体の質量には関係ない」事を証明した、ピサの斜塔の有名な実験がありますが、これはニュートンの法則からも説明できます。
自由落下時の物体にかかる力はmgとなり、質量に比例しているので一見重い方が早く落ちるかと思いますが、ニュートンの法則に当てはめると以下となり、
加速度は質量の項が消され、一定であることが解ります。
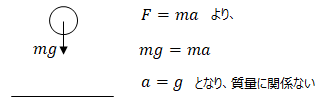
■万有引力
万有引力とは、物体同士が引き合う力の事で、以下で表す事ができます。
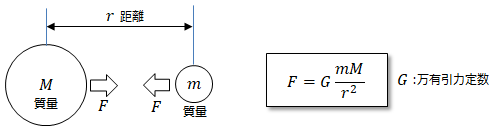
ニュートンは木からリンゴが落ちるのをみて万有引力を発見したと言われています。重力を発見したと思っている人もおりますが、それは間違いです。
では何故リンゴが落ちる事と万有引力の存在を結び付ける事ができたのでしょうか。それは地球とリンゴの引き合う関係は、例え距離が離れても同じであると考え、地球と惑星が引き合う関係も同じであると考えたからです。
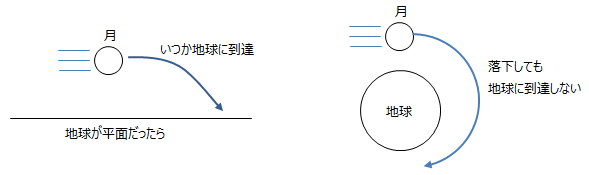
しかしリンゴにも惑星にも同じく万有引力が働いているなら、リンゴは落下するのになぜ惑星は落ちてこないのでしょうか。その理由は、惑星には万有引力が確かに働いており実際に落下しているのですが、地球は丸いという事と、月はものすごい速さで動いている事から、
落下し続けても地面に到達しないからです。万有引力と遠心力が釣り合っているという説明も正しくは有りません。※ リンゴの話は脚色が入っていると思いますが、リンゴの様には落下しない惑星に対して、万有引力の存在を認める発想は凄いと思いました。
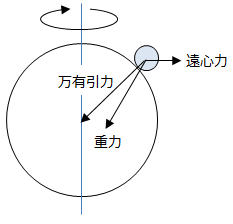
<万有引力と重力の違い>
重力と万有引力はどちらも物体が引き合う力なので、同じものの様に思うかもしれませんが、両者は異なります。万有引力は物体が引き合う力のみを指しているのに対し、重力は物体の引き合う力と遠心力が合わさったものを指しています。
従って力の向きは、万有引力は地球の中心であるのに対して、重力は厳密には地球の中心ではありません。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|