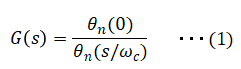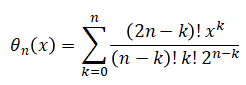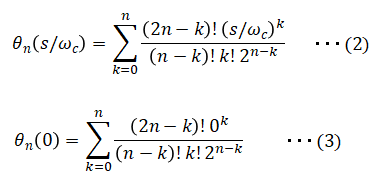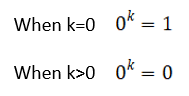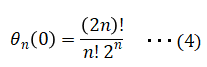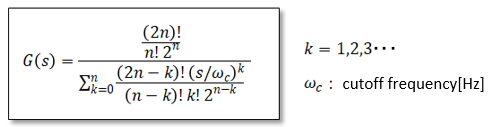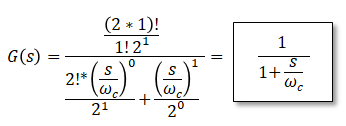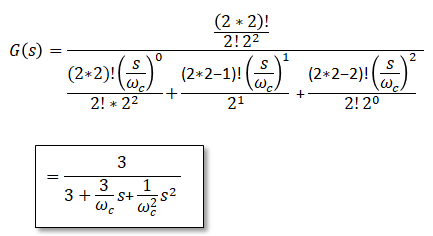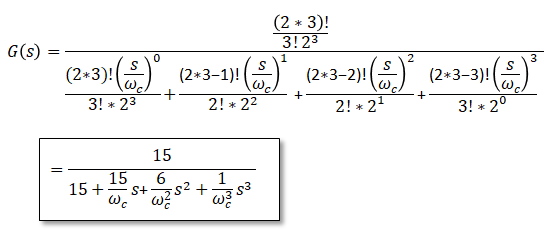What is Bessel Filter?

・In Japanese
＜Premise knowledge＞
・Transfer function
・Basics of how to draw Bode plots
・How to draw a Bode plot in Scilab

■What is Bessel Filter?

The Bessel filter has no ripple in the passband, and the gain decays smoothly from the flat region to the attenuation region. Therefore, it has characteristics that are easy to stabilize even in transient. On the other hand, the attenuation characteristic is gentler than that of the Butterworth filter, so it is not suitable for strong attenuation.

■Bessel filter transfer function

As below.


θ_n is called an inverse Bessel polynomial and is as follows.


Therefore,


Here, in equation (3), we can see that only k=0 takes a value.


Therefore, equation (3) is as follows.


Substituting (2) and (4) into (1) gives the final transfer function:



＜When n=1＞


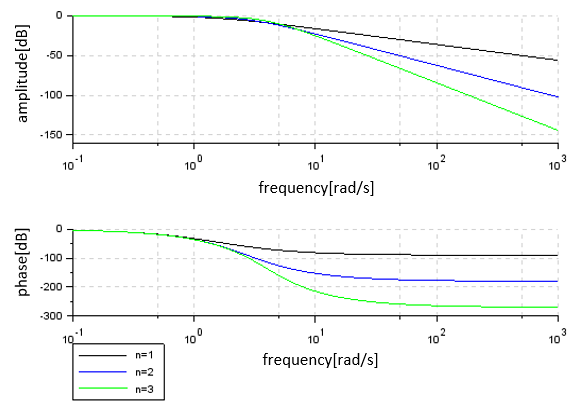
＜When n=2＞


＜When n=3＞

■Bode Plot of Bessel Filter

A Bode plot drawn in Scilab looks like this: set w_c=10.

==============================
s=poly(0,'s');
p=syslin('c',1/(s/10+1));
q=syslin('c',3/(s^2/10^2+3/10*s+3));
r=syslin('c',15/(s^3/10^3+6/10^2*s^2+15/10*s+15));
bode([p;q;r],0.1,1000,['n=1';'n=2';'n=3']);
==============================

List of related articles TOP MENU Control theory Transfer function Transfer function Transfer function synthesis Closed/Open-loop transfer function Analog filter Low Pass Filter ・First-order delay system 　・Transfer function 　・Bode plot ・secondary delay system 　・Bode plot ・Butterworth filter ・Bessel filter All pass filter 　・Transfer function 　・Pade approximation Notch filter Band pass filter