トップメニューデジタルフィルタとは, FIRフィルタとIIRフィルタの違い |
|||||||
2進数 16進数 浮動小数点 固定小数点 デジタル信号処理の基本- 分解能 , サンプリング周期 標本化定理 周波数分析・周波数分析の方法 ・フーリエ変換で自力計算 ・窓関数とは ・直流(DC)成分とは ・トレンド除去方法 ・オクターブ分析 デジタルフィルタ 差分方程式 双一次変換 |
・In English
■デジタルフィルタとは
デジタルフィルタとは、離散時間系におけるフィルタのことです。時間を離散系で扱う必要のある組み込み系などにおいてフィルタを実装する場合、連続時間系を離散化して実装します。
例えばローパスフィルタの連続時間系と離散時間系の違いのイメージは以下のとおり。
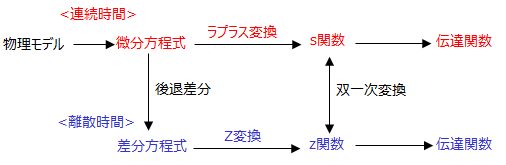
■離散化の方法
連続時間においては、物理モデルを微分方程式で表現し、それをラプラス変換してs関数に置き換えました。
離散時間においては、微分方程式を後退差分法などで表現し、それをZ変換してz関数に置き換える必要があります。
なお、s関数から双一次変換によってz関数に近似する手法もあります。 ■デジタルフィルタの種類
デジタルフィルタには大きく分けてFIR(Finite Impulse Response)フィルタとIIR(Infinite Impulse Response)フィルタがあります。
両者の違いは、FIRフィルタは入力値だけを使って処理するフィルタに対して、IIRフィルタは入力値だけではなく出力値も使ったフィルタとなります。
入力値しか使わないFIRは、入力が0になったらいずれは出力も0になるので、有限の(Finite)応答といえます。
一方、出力値も使うIIRは入力が0になっても結果が0になるとは限らないので無限の(Infinite)応答といいます。
・過去の入力情報を多く覚える必要があり、メモリー容量を必要とする。演算式も長くなる。
・多くの過去の入力情報は必要なく、簡単な式で表現することが可能。
■デジタルフィルタの動作確認こちらで説明します。
サブチャンネルあります。⇒ 何かのお役に立てればと
|
|
|||||
