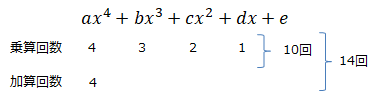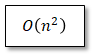アルゴリズムの計算量の求め方

プログラム実行時は、アルゴリズムの計算量が少ない方が実行時間が短くなるので良いとされてます。いざアルゴリズムを構築してみたら、計算量が多すぎて膨大な時間がかかり使い物にならなかったという事がない様に、あるいは計算量を減らす為どの部分に手を付けるべきかを検討できる様に、アルゴリズムの計算量を把握するという事は重要になります。ここではアルゴリズムの計算量の求め方を説明します。

具体例として以下多項式の計算量を考えます。乗算と加算を合わせて14回の計算量となります。

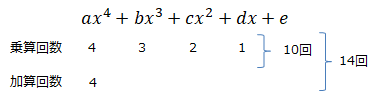
乗算回数はnを多項式の次数としたときに、以下等差数列の和で表すことができます。また加算回数はnと等しくなるので、総計算回数の一般解は以下となります。

＜補足＞
乗算と加算とでは計算に必要なステップ数が異なり、乗算の方が一般的に計算量が多くなります。従って厳密に計算量を求めようとするならば、乗算と加算に必要なステップ数から考える必要がありますが、ここでは考え方を理解出来るようにしたいので、乗算と加算を同列に考えております。あるいは加算を無視して乗算だけで考えても良いかもしれません。

■オーダー記法(ランダウのO記法)
上記(1)式において、計算量はnの値が大きくなるほどn²の部分が支配的となり、nの部分は無視できる様になります。この時およそn²に比例した計算量をもつアルゴリズムであるという意味で、以下の様な表記をします。これをランダウのO記法といいます。

　　
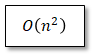
なお上記において、n²の係数部分も無視してます。それは主なO(x)の種類と、計算量のオーダーが多い順は以下となりますが、ここでそれぞれのxに係数をかけたとしても、この計算量のオーダーの序列が変わることは無いので、計算量を評価するうえで係数は考慮しなくても大勢に影響はないからです。

nに応じた計算量は以下となります。

＜具体例①:ホーナー法＞
先程説明したとおり、多項式の計算量はO(n²)となります。しかしホーナー法を用いると計算量をO(n)まで減らす事ができます。

＜具体例②：高速フーリエ変換＞
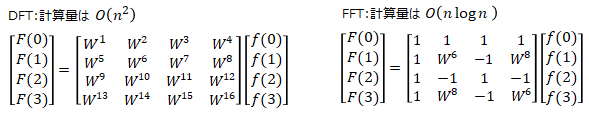
離散フーリエ変換(DFT)で行う行列計算の計算量は乗算のみでO(n²)となります。しかし高速フーリエ変換(FFT)を行うとO(nlogn)まで乗算を減らす事ができます。

＜具体例③：二分探索法＞
探索アルゴリズムの一つである線形探索法(一つずつ端から探していく手法)の計算量はO(n)ですが、二分探索法を用いたらO(logn)となります。

サブチャンネルあります。⇒ 何かのお役に立てればと