|
前提知識
・pythonとは
サポートベクターマシン(Support Vector Machine:SVM)の使い方を実例を踏まえて説明します。
題材は、ある昆虫の身長と体重からその個体がオスかメスかを分類します。

■SVMの考え方
SVMの考え方は、それぞれのデータに対してマージンを最大化できるところに線を引くという考え方です。

■pythonによるシミュレーション
scikit-learnというデータ分析に特化したライブラリの中にSVMがありますので、それを使ってみます。
・pythonバージョン:Ver3.8で確認
・必要ライブラリ:numpy,matplotlib,scikit-learn (インストール方法はこちら)
・必要ファイル:svm.zip(プログラムファイル, 訓練データ)
実行結果は以下の様に分類する事ができました。

■非線形の分類方法
非線形で分類する考え方を説明します。例えば以下の様なデータがあったとします。
これはこのままでは線形分類できないのが解ると思います。
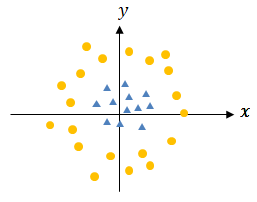
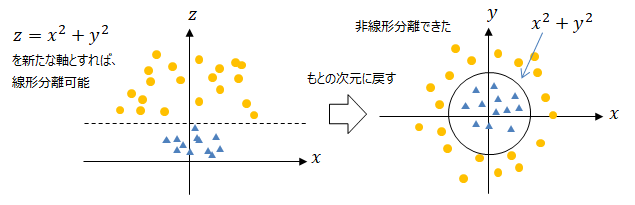
これを以下の様にZ軸(=x2+y2)という新たなパラメータで表すと線形分離できます。
この様に一度多次元空間に写像した状態で線形分離し、再びもとの低次元空間に戻すことで非線形分離が可能となります。
高次元空間への写像を行い線形分離を行う場合、内積(共分散)の計算が必要になり膨大な計算量になるのですが、これを容易に行う手法をカーネルトリックといい、
その際に使う関数をカーネル関数といいます。
■SVM適合パラメータ
scikit-learnには、もとのデータに対してどれだけ正確にフィッティングさせるか等を設定する機能があります。ただし、あまり厳密にフィッティングさせようとすると
境界線がいびつになり、テストデータに対しては適切に分類できなくなってきます。この状態をオーバーフィッティングといいます。主なパラメータは以下。
<kernel>
上記で説明したカーネル関数を設定します。主に以下があります。
linear:線形
poly:多項式
rbf:Radial basis function(放射基底関数) ここではガウスカーネルのこと
sigmoid:シグモイドカーネル
<gamma>
訓練データの位置を中心とした分布の広がり度合いを決める。値が小さいほど緩やかな分布になり、訓練データの感度が下がる。
値が大きいと鋭い分布になり訓練データの位置に過学習しやすくなる。
<C>
コストパラメータ。値が小さいほど誤りを許容し、大きいほど誤りを許容しなくなるので過学習しやすくなる。
■pythonによるシミュレーション②
・テストパラメータ:kernel=rbf , C=1000 , gamma=0.0001
・必要ファイル:svm2.zip(プログラムファイル, 訓練データ)
結果は以下のとおり、非線形の分類ができました。ただし訓練データに対して若干過剰にフィッティングされた状態となっています。

サブチャンネルあります。⇒ 何かのお役に立てればと
|
|





